题目内容
已知函数
(1)若 ,解不等式
,解不等式 ;
;
(2)解关于 的不等式
的不等式

(1)若
 ,解不等式
,解不等式 ;
;(2)解关于
 的不等式
的不等式
(1)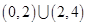
(2)当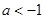 时,原不等式的解集为
时,原不等式的解集为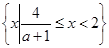 ;
;
当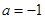 时,原不等式的解集为
时,原不等式的解集为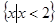 ;
;
当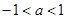 时,原不等式的解集为
时,原不等式的解集为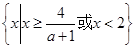 ;
;
当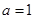 时,原不等式的解集为
时,原不等式的解集为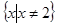 ;
;
当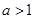 时,原不等式的解集为
时,原不等式的解集为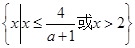 ;
;
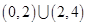
(2)当
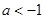 时,原不等式的解集为
时,原不等式的解集为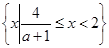 ;
;当
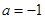 时,原不等式的解集为
时,原不等式的解集为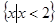 ;
;当
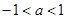 时,原不等式的解集为
时,原不等式的解集为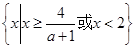 ;
;当
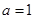 时,原不等式的解集为
时,原不等式的解集为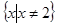 ;
;当
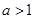 时,原不等式的解集为
时,原不等式的解集为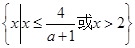 ;
;试题分析:解:(1)

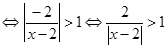
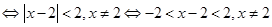 ,
,故解得原不等式的解集为
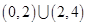 ; .4分
; .4分(2)原式
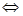
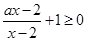
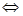
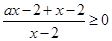
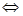
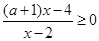
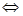
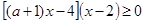 且
且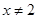 , 6分
, 6分当
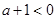 ,即
,即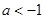 时,原不等式
时,原不等式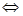
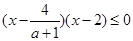 且
且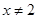 ,
,解得
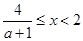 7分
7分当
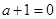 ,即
,即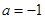 时,原不等式
时,原不等式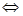
 8分
8分当
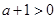 ,即
,即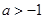 时,原不等式
时,原不等式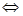
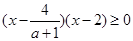 且
且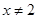 , 9分
, 9分?当
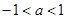 时,
时,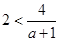 ,解出
,解出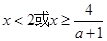 ;
;?当
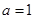 时,
时,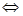
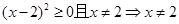 ; 10分
; 10分?当
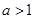 时,
时,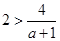 ,解出
,解出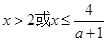 ; 11分
; 11分综上:当
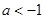 时,原不等式的解集为
时,原不等式的解集为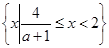 ;
;当
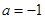 时,原不等式的解集为
时,原不等式的解集为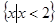 ;
;当
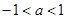 时,原不等式的解集为
时,原不等式的解集为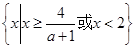 ;
;当
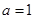 时,原不等式的解集为
时,原不等式的解集为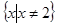 ;
;当
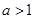 时,原不等式的解集为
时,原不等式的解集为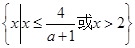 ; 12分
; 12分点评:主要是考查了一元二次不等式的解集的求解,以及分类讨论思想的运用,属于中档题。

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
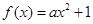 (
( ),
), .
. 与
与 处具有公共切线,求
处具有公共切线,求 的值;
的值; 时,求函数
时,求函数 在区间
在区间 上的最大值.
上的最大值.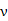 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度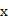 (单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当
(单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当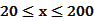 时,车流速度
时,车流速度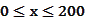 时,求函数
时,求函数 的表达式;
的表达式;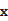 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)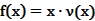 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时)
 时, 求函数
时, 求函数 的单调增区间;
的单调增区间; 上的最小值;
上的最小值;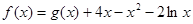 ,
, .参考数据:
.参考数据: .
. = ;
= ; ,在
,在 时取得极值.
时取得极值. 的解析式;
的解析式; 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围; ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间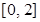 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由. ,定义
,定义 ,则函数
,则函数 是( )
是( )