题目内容
定义新运算⊕:当a ≥b时,a⊕b=a;当a<b时,a⊕b=b2,则f(x)=(1⊕x)x-(2⊕x),x∈[-2,2]的最小值等于 。

试题分析:由题意知,当
 时,
时, ,当
,当 时,
时, ,
,又
 ,
, 在定义域上都为增函数,
在定义域上都为增函数,所以
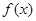 的最小值为
的最小值为
点评:本题考查分段函数,以及函数的最值及其几何意义,考查函数单调性及导数求最值,是基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
题目内容

 时,
时, ,当
,当 时,
时, ,
, ,
, 在定义域上都为增函数,
在定义域上都为增函数,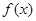 的最小值为
的最小值为

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案