题目内容
焦点坐标是 ,
, ,且虚轴长为
,且虚轴长为 的双曲线的方程是( )
的双曲线的方程是( )
A. | B. |
C. | D. |
C
解析试题分析:因为焦点为 ,
, ,所以焦点在x轴上且c=2,又因为虚轴长为
,所以焦点在x轴上且c=2,又因为虚轴长为 ,所以2b=2,即b=1,所以a=
,所以2b=2,即b=1,所以a=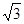 。所以双曲线方程为
。所以双曲线方程为 。
。
考点:双曲线的标准方程;双曲线的简单性质。
点评:本题容易出错的地方是:把虚轴长当成了b。实质上,虚轴长是2b。

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
抛物线  的准线方程是( )
的准线方程是( )
| A.4 x + 1 = 0 | B.4 y + 1 =" 0" |
| C.2 x + 1 = 0 | D.2 y + 1 =" 0" |
抛物线y2=2px(p>0)上有一点M,它的横坐标是3,它到焦点的距离是5,则抛物线方程为( A )
| A.y2=8x | B.y2=4x | C.y2=3x | D.y2=2x |
椭圆 上一点P到两焦点的距离之积为m,则m取最大值时P点坐标是( )
上一点P到两焦点的距离之积为m,则m取最大值时P点坐标是( )
| A.(0,3)或(0,-3) | B.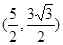 或 或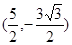 |
| C.(5,0)或(-5,0) | D. 或 或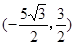 |
椭圆 的焦点在
的焦点在 轴上,长轴长是短轴长的两倍,则m的值为 ( )
轴上,长轴长是短轴长的两倍,则m的值为 ( )
A. | B. | C. | D. |
椭圆 上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于 的等差数列, 则n的最大值是( )
的等差数列, 则n的最大值是( )
| A.198 | B.199 | C.200 | D.201 |
如图所示,A,B,C分别为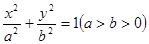 的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )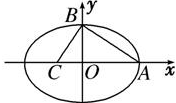
A.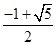 | B.1-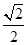 | C.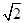 -1 -1 | D.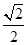 |
 、
、 是双曲线
是双曲线 的两焦点,点
的两焦点,点 在该双曲线上,且
在该双曲线上,且 是等腰三角形,则
是等腰三角形,则






