题目内容
如图,正方体 的棱长为
的棱长为 ,点
,点 在棱
在棱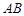 上, 且
上, 且 , 点
, 点 是平面
是平面 上的动点,且动点
上的动点,且动点 到直线
到直线  的距离与点
的距离与点 到点
到点 的距离的平方差为
的距离的平方差为 ,则动点
,则动点 的轨迹是( )
的轨迹是( )
| A.圆 | B.双曲线 | C.抛物线 | D.直线 |

C.
解析试题分析:以D为原点,以DA,DC,DD1所以直线为x,y,z轴建立直角坐标系D-xyz,设 ,
, ,因为动点
,因为动点 到直线
到直线 的距离与点P到点M的距离的平方差为1,所以
的距离与点P到点M的距离的平方差为1,所以 ,即
,即 ,所以点P的轨迹为抛物线.
,所以点P的轨迹为抛物线.
考点:求轨迹方程,空间直角坐标系,曲线与方程的关系.
点评:解本小题关键是建立空间直角坐标系,根据求得的点P的轨迹方程来确定其轨迹形状.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
抛物线 上一点P到
上一点P到 轴的距离是4,则点P到该抛物线焦点的距离是( )
轴的距离是4,则点P到该抛物线焦点的距离是( )
| A.4 | B.6 | C.8 | D.12 |
椭圆 的焦点在
的焦点在 轴上,长轴长是短轴长的两倍,则m的值为 ( )
轴上,长轴长是短轴长的两倍,则m的值为 ( )
A. | B. | C. | D. |
椭圆 上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于 的等差数列, 则n的最大值是( )
的等差数列, 则n的最大值是( )
| A.198 | B.199 | C.200 | D.201 |
双曲线 的焦点坐标为
的焦点坐标为
A. | B. | C. | D. |
 、
、 是双曲线
是双曲线 的两焦点,点
的两焦点,点 在该双曲线上,且
在该双曲线上,且 是等腰三角形,则
是等腰三角形,则







 的两个焦点,过F2的直线交椭圆于点A、B,若
的两个焦点,过F2的直线交椭圆于点A、B,若 ,
,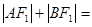 ( )
( ) 


