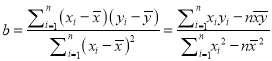题目内容
【题目】一个正整数，若它的每个质因数都至少是两重的（即每个质因数乘方次数都不小于2），则称该正整数为“漂亮数”.相邻两个正整数皆为“漂亮数”，就称它们是一对“孪生漂亮数”.例如8与9就是一对“孪生漂亮数”.请你再找出两对“孪生漂亮数”来.
【答案】见解析
【解析】
已知（8，9）是一对“孪生漂亮数”.
设（n，n + 1）是一对“孪生漂亮数”，由此可知4n（n + 1）也是个漂亮数.而
是个完全平方数，易知完全平方数必为漂亮数.
所以，
为一对“孪生漂亮数”.
于是，从
知
，
.
故（288，289）为一对“孪生漂亮数”.又取
，则
，
.
故
为另一对“孪生漂亮数”.
注：就本题目而言，只要指出两对“孪生漂亮数”就应算正确.如
，
；
，
，就是两对“孪生漂亮数”.如果本题设问为“证明：至少存在1989对孪生漂亮数”.这样题目的解答就必须推理证明了.
练习册系列答案
相关题目
