Question

【题目】定义在非零实数集上的函数满足，且是区间上的递增函数．

（1）求的值；

（2）求证： ；

（3）解不等式．

Answer 1

【答案】解：(1)令x=y=1，则f(1)="f(1)+" f(1) ∴f(1)=0

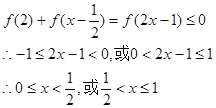
令x=y=－1，则f(1)=f(－1)+ f(－1) ∴f(－1)=0

(2)令y=－1，则f(－x)=f(x)+f(－1)="f(x) " ∴f(－x)=f(x)

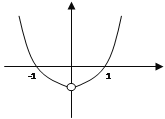
(3)据题意可知，函数图象大致如下：

【解析】试题分析：（1）根据，令可求得．（2）根据证明．（3）由可将变形为，由（1）可知，所以等价于．根据函数的单调性可得关于的不等式．

试题解析：解：（1）令，则

令，则

（2）令，则

，

∴为定义域上的偶函数．

（3）据题意可知，函数图象大致如下：

，

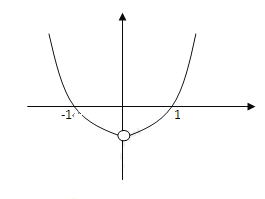
或，

或