题目内容
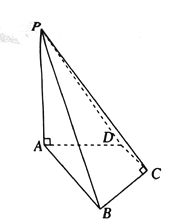
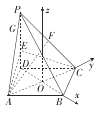
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上的一个点,
上的一个点, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)连接![]() ,取
,取![]() 的中点
的中点![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;(2)建立空间直角坐标系,求出平面
;(2)建立空间直角坐标系,求出平面![]() 的法向量,求得线面夹角的正弦值。
的法向量,求得线面夹角的正弦值。
试题解析:
(1)证明:连接![]() ,设
,设![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
在![]() 中,因为
中,因为![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
同理,在![]() 中,
中, ![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在的直线为
所在的直线为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
在等边三角形![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,
因此 ,
,
且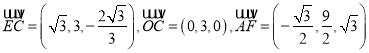 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则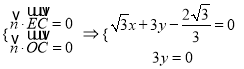 ,取
,取![]() ,得
,得![]() ,
,
直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则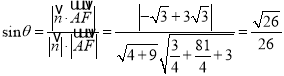 .
.

练习册系列答案
相关题目
【题目】随着互联网的发展,移动支付![]() 又称手机支付
又称手机支付![]() 逐渐深入人民群众的生活
逐渐深入人民群众的生活![]() 某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对
某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对![]() 岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表
岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表![]() 部分数据模糊不清
部分数据模糊不清![]() 如表:
如表:
分组 | 频数 | 频率 | |
第1组 |
| 10 |
|
第2组 |
|
|
|
第3组 |
| 15 |
|
第4组 |
|
|
|
第5组 |
| 2 |
|
合计 | 50 |
| |
![]() 表中
表中![]() 处的数据分别是多少?
处的数据分别是多少?
![]() 从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
![]() 在
在![]() 抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.