题目内容
判断下列对应是否是从集合A到集合B的函数.
(1) A=B=N*,对应法则f:x→y=|x-3|,x∈A,y∈B;
(2) A=[0,+∞),B=R,对应法则f:x→y,这里y2=x,x∈A,y∈B;
(3) A=[1,8],B=[1,3],对应法则f:x→y,这里y3=x,x∈A,y∈B;
(4) A={(x,y)|x、y∈R},B=R,对应法则:对任意(x,y)∈A,(x,y)→z=x+3y,z∈B.
(1) A=B=N*,对应法则f:x→y=|x-3|,x∈A,y∈B;
(2) A=[0,+∞),B=R,对应法则f:x→y,这里y2=x,x∈A,y∈B;
(3) A=[1,8],B=[1,3],对应法则f:x→y,这里y3=x,x∈A,y∈B;
(4) A={(x,y)|x、y∈R},B=R,对应法则:对任意(x,y)∈A,(x,y)→z=x+3y,z∈B.
(1)不是(2)不是(3)符合(4)不是
(1) 对于A中的元素3,在f的作用下得到0,但0不属于B,即3在B中没有元素与之对应,所以不是函数.
(2) 集合A中的一个正数在集合B中有两个元素与之对应,所以不是函数.
(3) 由y3=x,即y=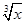 ,因为A=[1,8],B=[1,3],对应法则f:x→y,符合函数对应.
,因为A=[1,8],B=[1,3],对应法则f:x→y,符合函数对应.
(4) 由于集合A不是数集,所以此对应法则不是函数.
(2) 集合A中的一个正数在集合B中有两个元素与之对应,所以不是函数.
(3) 由y3=x,即y=
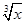 ,因为A=[1,8],B=[1,3],对应法则f:x→y,符合函数对应.
,因为A=[1,8],B=[1,3],对应法则f:x→y,符合函数对应.(4) 由于集合A不是数集,所以此对应法则不是函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
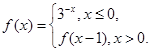 若
若 有且仅有三个解,则实数
有且仅有三个解,则实数 的取值范围是
的取值范围是 )图象上一动点,记m=
)图象上一动点,记m=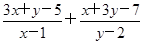 ,则当m最小时,点P的坐标为________.
,则当m最小时,点P的坐标为________.

 ,x∈[-1,8],函数g(x)=ax+2,x∈[-1,8],若存在x∈[-1,8],使f(x)=g(x)成立,则实数a的取值范围是________.
,x∈[-1,8],函数g(x)=ax+2,x∈[-1,8],若存在x∈[-1,8],使f(x)=g(x)成立,则实数a的取值范围是________. ,若
,若 ,
, ,则
,则 与
与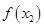 的大小关系为___________.
的大小关系为___________.