题目内容
【题目】数列![]() 中,
中,![]() ,
,![]() .前
.前![]() 项和
项和![]() 满足
满足![]() .
.
(1)求![]() (用
(用![]() 表示);
表示);
(2)求证:数列![]() 是等比数列;
是等比数列;
(3)若![]() ,现按如下方法构造项数为
,现按如下方法构造项数为![]() 的有穷数列
的有穷数列![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .记数列
.记数列![]() 的前
的前![]() 项和
项和![]() ,试问:
,试问:![]() 是否能取整数?若能,请求出
是否能取整数?若能,请求出![]() 的取值集合:若不能,请说明理由.
的取值集合:若不能,请说明理由.
【答案】(1)![]()
(2)证明见详解.
(3)![]() 能取整数,此时
能取整数,此时![]() 的取值集合为
的取值集合为![]() .
.
【解析】
(1)利用递推关系式,令![]() ,通过
,通过![]() ,
,![]() 求出
求出![]() 即可.
即可.
(2)递推关系式转化为:![]() ,化简推出数列
,化简推出数列![]() 是等比数列.
是等比数列.
(3)由![]() ,求出
,求出![]() ,求出
,求出![]() ,得到通项公式,然后求解
,得到通项公式,然后求解![]() 的分母与分子,讨论要使
的分母与分子,讨论要使![]() 取整数,需
取整数,需![]() 为整数,推出
为整数,推出![]() 的取值集合为
的取值集合为![]() 时,
时,![]() 取整数
取整数
解:(1)令![]() ,则
,则![]() ,
,
将![]() ,
,![]() 代入,有
代入,有![]() .
.
解得:![]() .
.
(2)由![]()
得![]() ,
,
化简得![]() ,又
,又![]() ,
,
![]() 是等比数列.
是等比数列.
(3)由![]() ,
,![]() ,
,
又![]() 是等比数列,
是等比数列,
![]() ,
,
![]() ,
,
①当![]() 时,
时,
![]() 依次为
依次为![]() ,
,
![]() .
.
②当![]() 时,
时,
![]() ,
,
![]() ,
,
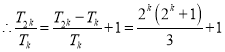 ,
,
要使![]() 取整数,需
取整数,需![]() 为整数,
为整数,
令![]() ,
,![]() ,
,
![]() ,
,![]() 要么都为整数,要么都不是整数,
要么都为整数,要么都不是整数,
又![]()
所以当且仅当![]() 为奇数时,
为奇数时,![]() 为整数,
为整数,
即![]() 的取值集合为
的取值集合为![]() 时,
时,![]() 取整数.
取整数.

【题目】历史数据显示:某城市在每年的3月11日—3月15日的每天平均气温只可能是-5℃,-6℃,-7℃,-8℃中的一个,且等可能出现.
(Ⅰ)求该城市在3月11日—3月15日这5天中,恰好出现两次-5℃,一次-8℃的概率;
(Ⅱ)若该城市的某热饮店,随平均气温的变化所售热饮杯数如下表
平均气温t | -5℃ | -6℃ | -7℃ | -8℃ |
所售杯数y | 19 | 22 | 24 | 27 |
根据以上数据,求![]() 关于
关于![]() 的线性回归直线方程.
的线性回归直线方程.
(参考公式: ,
,![]() )
)
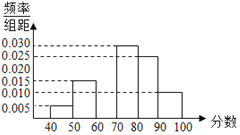
【题目】支付宝和微信支付是目前市场占有率较高的支付方式,某第三方调研机构对使用这两种支付方式的人数作了对比.从全国随机抽取了100个地区作为研究样本,计算了各个地区样本的使用人数,其频率分布直方图如图.
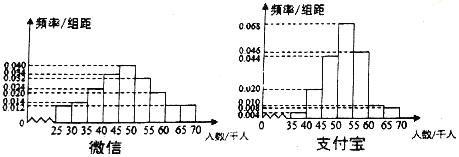
(1)记A表示事件“微信支付人数低于50千人”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为支付人数与支付方式有关;
支付人数<50千人 | 支付人数≥50千人 | 总计 | |
微信支付 | |||
支付宝支付 | |||
总计 |
(3)根据支付人数的频率分布直方图,对两种支付方式的优劣进行比较.
附:
P(K2≥K) | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2=![]()