Question

【题目】①在中，若，，，则此三角形的解的情况是两解．

②数列满足，，则．

③在中，为中线上的一个动点，若，则的最小值是．

④已知，则．

⑤已知等比数列的前项和为，则，，成等比数列．

以上命题正确的有______（只填序号）．

Answer 1

【答案】①

【解析】

根据三角形解得个数的判定方法，可判定①正确；由等比数列的定义和通项公式，可判定②不正确；由向量的数量积的运算，可判定③不正确；由数列的递推公式求解数列的通项公式，可判定④不正确；举出反例，可判定⑤不正确.

对于①中，由，可得，

因为，所以有两解，故①正确；

对于②中，由，可得，即，

所以数列构成首项为，公比为2的等比数列，所以，

即，所以，故②不正确；

对于③中，设，其中，则,

由为中线上的一个动点，若，

则

，

当时，取得最小值，最小值为，故③不正确；

对于④中，由，

则，

两式相减，可得，所以，

当时，可得，不适合上式，

所以数列的通项公式为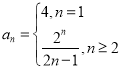，故④不正确；

对于⑤中，例如；等比数列为：时，可得，，，此时不能构成等比数列，故⑤不正确.

故答案为：①.