题目内容
【题目】已知数列{an}满足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)设![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式.
,求证:数列{bn}是等差数列,并求出{an}的通项公式.
(2)设![]() ,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得
,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得![]() 对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
【答案】(1)![]() ;(2)3
;(2)3
【解析】试题分析:
(1)结合递推关系可证得bn+1-bn![]() 2,且b1=2,即数列{bn}是首项为2,公差为2的等差数列,据此可得数列
2,且b1=2,即数列{bn}是首项为2,公差为2的等差数列,据此可得数列![]() 的通项公式为
的通项公式为![]() .
.
(2)结合通项公式裂项有![]() 求和有
求和有![]() .据此结合单调性讨论可得正整数m的最小值为3.
.据此结合单调性讨论可得正整数m的最小值为3.
试题解析:
(1)证明:bn+1-bn![]()
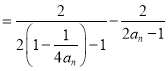
![]() .
.
又由a1=1,得b1=2,所以数列{bn}是首项为2,公差为2的等差数列,所以bn=2+(n-1)×2=2n,由![]() ,得
,得![]() .
.
(2)解: ![]() ,
, ![]() 所以
所以![]() .
.
依题意,要使![]() 对于n∈N*恒成立,只需
对于n∈N*恒成立,只需![]() ,解得m≥3或m≤-4.又m>0,所以m≥3,所以正整数m的最小值为3.
,解得m≥3或m≤-4.又m>0,所以m≥3,所以正整数m的最小值为3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料。试求:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
⑴画出数据的散点图,并判断y与x是否呈线性相关关系.
⑵若y与x呈线性相关关系,求线性回归方程 y = bx + a 的回归系数a、b;
⑶估计使用年限为10年时,维修费用是多少?
(参考数据: ,
,![]() ,
,![]() ,
,![]() )
)

