题目内容
【题目】公元263年左右，我国数学有刘徽发现当圆内接多边形的边数无限增加时，多边形的面积可无限逼近圆的面积，并创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的“徽率”．某同学利用刘徽的“割圆术”思想设计了一个计算圆周率的近似值的程序框图如图，则输出S的值为 （参考数据：sin15°=0.2588，sin7.5°=0.1305）（ ）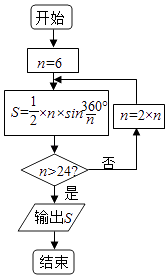
A.2.598
B.3.106
C.3.132
D.3.142
【答案】C
【解析】解：模拟执行程序，可得：
n=6，S=3sin60°= 
，
不满足条件n＞24，n=12，S=6×sin30°=3，
不满足条件n＞24，n=24，S=12×sin15°=12×0.2588=3.1056，
不满足条件n＞24，n=48，S=24×sin7.5°=24×0.1305=3.132，
满足条件n＞24，退出循环，输出S的值为3.132．
故选：C．
【考点精析】本题主要考查了程序框图的相关知识点，需要掌握程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明才能正确解答此题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）+B，A＞0，ω＞0，|φ|＜ 
在某一个周期的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x | x1 |
| x2 |
| x3 |
Asin（ωx+φ）+B | 0 |
| 0 | ﹣ | 0 |
（1）请求出上表中的x1 ， x2 ， x3 ， 并直接写出函数f（x）的解析式；
（2）若3sin2 
﹣ 
mf（ 
﹣ 
）≥m+2对任意x∈[0，2π]恒成立，求实数m的取值范围．
