题目内容
【题目】如图所示，在正三棱柱ABC﹣A1B1C1中，点D在边BC上，AD⊥C1D．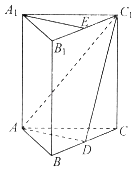 
（1）求证：平面ADC1⊥平面BCC1B1；
（2）如果点E是B1C1的中点，求证：AE∥平面ADC1 ．
【答案】
（1）证明：∵在正三棱柱ABC﹣A1B1C1中，点D在边BC上，AD⊥C1D，
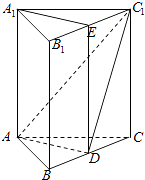
∴CC1⊥平面ABC，又AD平面ABC，∴AD⊥CC1，
又C1D∩CC1=C1，∴AD⊥平面BCC1B1．
AD面ADC1，∴平面ADC1⊥平面BCC1B1
（2）解：∵AD⊥平面BCC1B1，∴AD⊥BC，
∵在正三棱柱ABC﹣A1B1C1中，AB=BC=AC，∴D是BC中点，
连结ED，∵点E是C1B1的中点，
∴AA1∥DE且AA1=DE，∴四边形AA1DE是平行四边形，
∴A1E∥AD，
又A1E面ADC1，AD平面ADC1．
∴A1E∥平面ADC1．
【解析】（1）推导出AD⊥C1D，从而CC1⊥平面ABC，进而AD⊥CC1，由此能证明AD⊥平面BCC1B1．即平面ADC1⊥平面BCC1B1（2）由AD⊥BC，得D是BC中点，连结ED，得四边形AA1DE是平行四边形，由此能证明A1E∥平面ADC1．
【考点精析】根据题目的已知条件，利用直线与平面平行的判定和平面与平面垂直的判定的相关知识可以得到问题的答案，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一个平面过另一个平面的垂线，则这两个平面垂直．
应用题天天练四川大学出版社系列答案
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）+B，A＞0，ω＞0，|φ|＜ 
在某一个周期的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x | x1 |
| x2 |
| x3 |
Asin（ωx+φ）+B | 0 |
| 0 | ﹣ | 0 |
（1）请求出上表中的x1 ， x2 ， x3 ， 并直接写出函数f（x）的解析式；
（2）若3sin2 
﹣ 
mf（ 
﹣ 
）≥m+2对任意x∈[0，2π]恒成立，求实数m的取值范围．
