题目内容
12.已知函数f(x)=2ex-ax-2(a∈R)(1)若a=2,求证:f(x)≥0.
(2)若x∈[1,2],求f(x)的最小值.
(3)设函数y=f(x)图象上任意不同的两点A(x1,y1),B(x2,y2)且x1<x2,记直线AB的斜率为k,求证:k>f′(px1+qx2)(其中正常数p,q满足p+q=1且p≥q)
分析 (1)求出导数,求得单调区间和极小值,也为最小值,即可得证;
(2)求出导数,讨论当a≤2e,当a≥2e2,当2e<a<2e2时,求得单调区间,可得最小值;
(3)根据题意,由直线的斜率公式可得k,令φ(x)=f′(x)-k=2ex-a-2•$\frac{{e}^{{x}_{1}}-{e}^{{x}_{2}}}{{x}_{1}-{x}_{2}}$+a=2(ex-$\frac{{e}^{{x}_{1}}-{e}^{{x}_{2}}}{{x}_{1}-{x}_{2}}$),可以求出φ(x1)与φ(x2)的值,令F(t)=et-t-1,求导可得F′(t)=et-1,分t>0与t<0讨论可得F(t)的最小值为F(0)=0,则当t≠0时,F(t)>F(0)=0,即et-t-1>0,进而讨论可得φ(x1)<0、φ(x2)>0,结合函数的连续性分析可得答案.
解答 解:(1)证明:函数f(x)=2ex-2x-2的导数为f′(x)=2ex-2,
当x>0时,f′(x)>0,f(x)递增;当x<0时,f′(x)<0,f(x)递减.
当x=0处时,f(x)取得极小值,也为最小值,且为0,
即有f(x)≥0;
(2)函数f(x)=2ex-ax-2的导数为f′(x)=2ex-a,
由x∈[1,2],可得2ex∈[2e,2e2],
当a≤2e,即有f′(x)≥0,f(x)在[1,2]递增,
即有f(1)取得最小值2e-a-2;
当a≥2e2,即有f′(x)≤0,f(x)在[1,2]递减,
即有f(1)取得最小值2e2-2a-2;
当2e<a<2e2时,x>ln$\frac{a}{2}$,f′(x)>0,f(x)递增,
x<ln$\frac{a}{2}$时,f′(x)<0,f(x)递减,
即有x=ln$\frac{a}{2}$处取得极小值,也为最小值a-aln$\frac{a}{2}$-2;
(3)证明:由题意知,k=$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$=2•$\frac{{e}^{{x}_{1}}-{e}^{{x}_{2}}}{{x}_{1}-{x}_{2}}$-a.
由x1<x=px1+qx2<x2,
令φ(x)=f′(x)-k=2ex-a-2•$\frac{{e}^{{x}_{1}}-{e}^{{x}_{2}}}{{x}_{1}-{x}_{2}}$+a=2(ex-$\frac{{e}^{{x}_{1}}-{e}^{{x}_{2}}}{{x}_{1}-{x}_{2}}$),
则φ(x1)=-$\frac{{e}^{{x}_{1}}}{{x}_{2}-{x}_{1}}$[${e}^{{x}_{2}-{x}_{1}}$-(x2-x1)-1],φ(x2)=$\frac{{e}^{{x}_{2}}}{{x}_{2}-{x}_{1}}$[${e}^{{x}_{1}-{x}_{2}}$-(x1-x2)-1].
令F(t)=et-t-1,则F'(t)=et-1.
当t<0时,F'(t)<0,F(t)单调递减;当t>0时,F'(t)>0,F(t)单调递增.
故当t=0,F(t)>F(0)=0,即et-t-1>0.
从而${e}^{{x}_{2}-{x}_{1}}$-(x2-x1)-1>0,[${e}^{{x}_{1}-{x}_{2}}$-(x1-x2)-1>0,
又$\frac{{e}^{{x}_{1}}}{{x}_{2}-{x}_{1}}$>0,$\frac{{e}^{{x}_{2}}}{{x}_{2}-{x}_{1}}$>0,所以φ(x1)<0,φ(x2)>0.
因为函数y=φ(x)在区间[x1,x2]上的图象是连续不断的一条曲线,
且p≥q,即有px1+qx2与x1靠近,
即有k>f′(px1+qx2).
点评 本题考查导数的应用,涉及最大值、最小值的求法以及恒成立问题,是综合题;关键是理解导数的符号与单调性的关系,并能正确求出函数的导数.

 通城学典默写能手系列答案
通城学典默写能手系列答案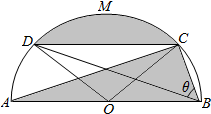 如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.
如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.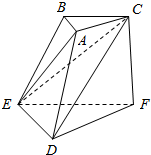 如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.