题目内容
10.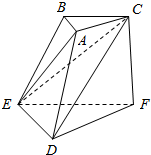 如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.(Ⅰ)设平面AEC∩平面DEF=a,求证:DF∥a;
(Ⅱ)求异面直线AE与CF所成的角的余弦值.
分析 (Ⅰ)假设DF与a不平行,则DF与a有交点,设为P,由公理二得AC与DF相交,与已知AC∥DF矛盾,从而假设不成立,即DF∥a.
(Ⅱ)以F为原点,FE为x轴,FD为y轴,FC为z轴,建立空间直角坐标系,利用向量法能求出异面直线AE与CF所成的角的余弦值.
解答  (Ⅰ)证明:∵平面AEC∩平面DEF=a,∴DE与α共面于平面DEF,
(Ⅰ)证明:∵平面AEC∩平面DEF=a,∴DE与α共面于平面DEF,
假设DF与a不平行,则DF与a有交点,设为P,
∵三棱台ABC-DEF中,DF∥AC,∴AC∩a=P,
由公理二得AC∩DF=P,与已知AC∥DF矛盾,
∴假设不成立,即DF∥a.
(Ⅱ)解:∵三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC,
∴以F为原点,FE为x轴,FD为y轴,FC为z轴,建立空间直角坐标系,
设DF=EF=CF=2AC=2,
则A(0,1,2),E(2,0,0),C(0,0,2),F(0,0,0),
∴$\overrightarrow{AE}$=(2,-1,-2),$\overrightarrow{CF}$=(0,0,-2),
设异面直线AE与CF所成的角为θ,
则cosθ=|cos<$\overrightarrow{AE},\overrightarrow{CF}$>|=|$\frac{\overrightarrow{AE}•\overrightarrow{CF}}{|\overrightarrow{AE}|•|\overrightarrow{CF}|}$|=|$\frac{4}{\sqrt{9}×2}$|=$\frac{2}{3}$,
∴异面直线AE与CF所成的角的余弦值为$\frac{2}{3}$.
点评 本题考查两直线平行的证明,考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意反证法和向量法的合理运用.

| A. | x2+y2-x-2y-$\frac{1}{4}$=0, | B. | x2+y2+x-2y+1=0, | ||
| C. | x2+y2-x+1=0, | D. | x2+y2-x-2y+$\frac{1}{4}$=0, |
| A. | 四棱锥 | B. | 圆柱 | C. | 长方体 | D. | 三棱柱 |
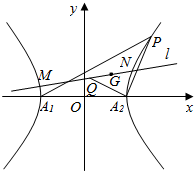 已知中心在原点,左、右顶点A1、A2在x轴上,离心率为$\frac{\sqrt{21}}{3}$的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点.
已知中心在原点,左、右顶点A1、A2在x轴上,离心率为$\frac{\sqrt{21}}{3}$的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点.