题目内容
已知O为坐标原点,A,B两点的坐标均满足不等式组
,则tan∠AOB的最大值等于( )
|
分析:先根据约束条件画出可行域,只需求出A,B在图中的位置,∠AOB最大,即tan∠AOB最大即可.
解答: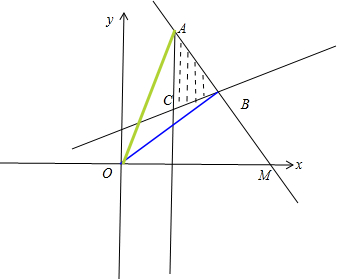 解:作出可行域,则A、B在图中所示的位置时,∠AOB最大,即tan∠AOB最大,
解:作出可行域,则A、B在图中所示的位置时,∠AOB最大,即tan∠AOB最大,
由题意可得A(1,,2),B(2,1)
∴KOA=tan∠AOM=2,KOB=tan∠BOM=
∵∠AOB=∠AOM-∠BOM,
∴tan∠AOB=tan(∠AOM-∠BOM)
=
=
=
,
所以tan∠AOB的最大值为
故选B
 解:作出可行域,则A、B在图中所示的位置时,∠AOB最大,即tan∠AOB最大,
解:作出可行域,则A、B在图中所示的位置时,∠AOB最大,即tan∠AOB最大,由题意可得A(1,,2),B(2,1)
∴KOA=tan∠AOM=2,KOB=tan∠BOM=
| 1 |
| 2 |
∵∠AOB=∠AOM-∠BOM,
∴tan∠AOB=tan(∠AOM-∠BOM)
=
| tan∠AOM-tan∠BOM |
| 1+tan∠AOMtan∠BOM |
=
2-
| ||
1+2×
|
=
| 3 |
| 4 |
所以tan∠AOB的最大值为
| 3 |
| 4 |
故选B
点评:借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.线性规划中的最优解,通常是利用平移直线法确定.巧妙识别目标函数的几何意义是我们研究规划问题的基础.

练习册系列答案
相关题目