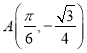Question

【题目】若曲线和上分别存在点,使得是以原点为直角顶点的直角三角形，AB交y轴于C,且则实数的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

由题意设出A，B的坐标，代入函数解析式，利用把B的坐标用A的坐标表示，由可得关于A的横坐标的方程，分离参数a后构造函数h（x），利用导数求其在（e﹣1＜x＜e2﹣1）上的单调性，得到函数的值域得答案．

设A（x1，y1），y1＝f（x1），B（x2，y2），y2＝g（x2）＝﹣x23+x22（x＜0），又，

则，x2＝﹣2x1，∴．

，，

由题意，，即0，

∴，

∵e﹣1＜x1＜e2﹣1，

∴，

则．

设h（x），则h′（x），令,则u′（x）==>0在e﹣1＜x＜e2﹣1恒成立，所以单增，所以>=>0，∴h′（x）＞0，

即函数h（x）在（e﹣1＜x＜e2﹣1）上为增函数，

则，

即4e-2＜a．

∴实数a的取值范围是．

故选：B．