Question

【题目】已知，，其中，，且函数在处取得最大值.

（1）求的最小值，并求出此时函数的解析式和最小正周期；

（2）在(1)的条件下，先将的图像上的所有点向右平移个单位，再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变)，然后将所得图像上所有的点向下平移个单位，得到函数的图像.若在区间上，方程有两个不相等的实数根，求实数a的取值范围；

（3）在(1)的条件下，已知点P是函数图像上的任意一点，点Q为函数图像上的一点，点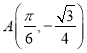，且满足，求的解集.

Answer 1

【答案】（1）的最小值为1，，，（2）（3）原不等式的解集为

【解析】

（1）先将化成正弦型，然后利用在处取得最大值求出，然后即可得到的解析式和周期

（2）先根据图象的变换得到，然后画出在区间上的图象，条件转化为的图象与直线有两个交点即可

（3）利用坐标的对应关系式，求出的函数的关系式，进一步利用三角不等式的应用求出结果．

（1）因为，

所以

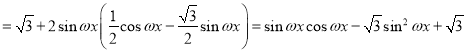
因为在处取得最大值.

所以，即

当时的最小值为1

此时，

（2）将的图像上的所有的点向右平移个单位得到的函数为，再把所得图像上所有的点的横坐标伸长为原来的2倍(纵坐标不变)得到的函数为，然后将所得图像上所有的点向下平移个单位，得到函数

在区间上的图象为：

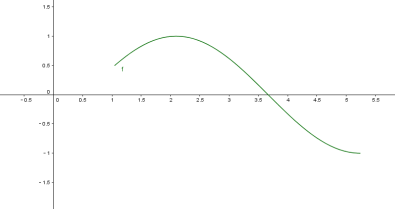
方程有两个不相等的实数根等价于的图象

与直线有两个交点

所以，解得

（3）设，

因为点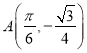，且满足

所以，所以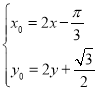

因为点为函数图像上的一点

所以

即

因为，所以

所以

所以

所以原不等式的解集为