题目内容
13.在△ABC中,AB=4,∠ABC=30°,D是边BC上的一点,且$\overrightarrow{AD}$•$\overrightarrow{AB}$=$\overrightarrow{AD}$•$\overrightarrow{AC}$,则$\overrightarrow{AD}$•$\overrightarrow{AB}$的值等于4.分析 根据$\overrightarrow{AD}$•$\overrightarrow{AB}$=$\overrightarrow{AD}$•$\overrightarrow{AC}$,可推得AD⊥CB,通过解直角三角形可得AD=2及∠BAD=60°,由数量积定义可求答案.
解答 解:由$\overrightarrow{AD}$•$\overrightarrow{AB}$=$\overrightarrow{AD}$•$\overrightarrow{AC}$,
得$\overrightarrow{AD}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=0,
即$\overrightarrow{AD}$•$\overrightarrow{CB}$=0,
∴$\overrightarrow{AD}$⊥$\overrightarrow{CB}$,即AD⊥CB,
又AB=4,∠ABC=30°,
∴AD=AB×sin30°=2,∠BAD=60°,
∴$\overrightarrow{AD}$•$\overrightarrow{AB}$=AD×ABcos∠BAD=2×4×cos60°=4,
故答案为:4.
点评 本题考查平面向量数量积的运算及其定义,属基础题.熟练掌握数量积的运算性质是解决相关问题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
4.|z-5+12i|≤2,则|z|的最小值为( )
| A. | 7 | B. | 9 | C. | 11 | D. | 15 |
5.以下选项中正确的是( )
| A. | a=7,b=14,A=30°△ABC有两解 | B. | a=9,c=10,A=60°△ABC无解 | ||
| C. | a=6,b=9,A=45°△ABC有两解 | D. | a=30,b=25,A=150°△ABC有一解 |
3.为了解某班关注NBA是否与性别有关,对该班48人进行了问卷调查得到如下的列联表:
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为$\frac{2}{3}$
(1)请将右面的表补充完整(不用写计算过程,但要将表格画在答题纸上);
(2)判断是否有95%的把握认为关注NBA与性别有关?
下面的临界值表,供参考
| 关注NBA | 不关注NBA | 合计 | |
| 男生 | 6 | ||
| 女生 | 10 | ||
| 合计 | 48 |
(1)请将右面的表补充完整(不用写计算过程,但要将表格画在答题纸上);
(2)判断是否有95%的把握认为关注NBA与性别有关?
下面的临界值表,供参考
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 60.635 | 7.879 |
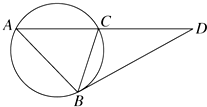 过D作圆的切线切于B点,作割线交圆于A、C两点,若BD=3,AD=4,AB=2,则BC=$\frac{3}{2}$.
过D作圆的切线切于B点,作割线交圆于A、C两点,若BD=3,AD=4,AB=2,则BC=$\frac{3}{2}$.