题目内容
6．若复数|z-3-4i|=1，求|z|的最大值，最小值，并求最值时的z．分析 复数z满足|z-3-4i|=2，其几何意义为：z对应的点在以（3，4）为圆心，1为半径的圆上，从而可求|z|的最值．求出最值时的z即可．
解答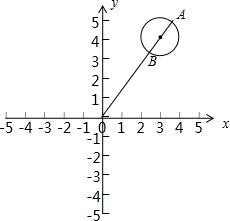 
解：∵复数z满足|z-3-4i|=1，
∴z对应的点在以P（3，4）为圆心，1为半径的圆上，
则|z|max=5+1=6．
|z|min=5-1=4．
取得最大值时A点，$\overrightarrow{OA}=\frac{6}{5}\overrightarrow{OP}$，可得$\frac{6}{5}（3，4）$=$（\frac{18}{5}，\frac{24}{5}）$，A$（\frac{18}{5}，\frac{24}{5}）$．
取得最小值时为B点，$\overrightarrow{OB}=\frac{4}{5}（3，4）$，可得B$（\frac{12}{5}，\frac{16}{5}）$．
点评 本题考查复数的几何意义，考查复数的模，属于中档题．
练习册系列答案
相关题目
14．下列说法正确的是（ ）
| A． | 一条直线垂直于三角形的两条边，则该直线与三角形所在平面垂直 | |
| B． | 一条直线垂直于梯形的两条边，则该直线与梯形所在平面垂直 | |
| C． | 一条直线垂直于平面内无数多条直线，则该直线与平面垂直 | |
| D． | 两条平行线中一条垂直于一个平面，另一条不一定垂直于这个平面 |
11．已知等差数列{an}的首项为4，公差为4，其前n项和为Sn，则数列的前n项和的倒数为（ ）
| A． | $\frac{n}{2（n+1）}$ | B． | $\frac{1}{2n（n+1）}$ | C． | $\frac{2}{n（n+1）}$ | D． | $\frac{2n}{n+1}$ |