题目内容
【题目】在梯形
中，
．将梯形绕
所在的直线旋转一周而形成的曲面所围成的几何体的表面积为_______．
【答案】
【解析】
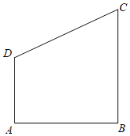
将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体是：一个底面半径为AB＝1，高为BC＝2的圆柱减去一个底面半径为AB＝1，高为BC﹣AD＝2﹣1＝1的圆锥，由此能求出该几何体的表面积．
∵在梯形ABCD中，∠ABC
，AD∥BC，BC＝2AD＝2AB＝2，
∴将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体是：
一个底面半径为AB＝1，高为BC＝2的圆柱减去一个底面半径为AB＝1，
高为BC﹣AD＝2﹣1＝1的圆锥，
∴几何体的表面积为：
S＝π×12+2π×1×2
＝（5
）π．
故选：D．
练习册系列答案
相关题目
