题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,侧面
是边长为2的正方形,侧面![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,侧面
,侧面![]() ⊥底面
⊥底面![]() .
.
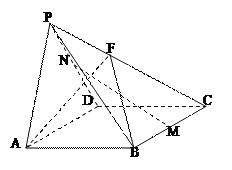
(1)若![]() 分别为棱
分别为棱![]() 的中点,求证:
的中点,求证:![]() ∥平面
∥平面![]() ;
;
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 成
成![]() 角,若存在,求出
角,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)见解析( 2) ![]()
【解析】
分析:(1)取![]() 中点
中点![]() ,连结
,连结![]() ,由三角形中位线定理可得
,由三角形中位线定理可得![]() ,可证明四边形
,可证明四边形![]() 为平行四边形,可得
为平行四边形,可得![]() ,由线面平行的判定定理可得结论;(2)取
,由线面平行的判定定理可得结论;(2)取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,先证明
,先证明![]() 、
、![]() 、
、![]() 两两垂直. 以
两两垂直. 以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 正方向为
正方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向建立空间直角坐标系,设
轴正方向建立空间直角坐标系,设![]() ,利用向量垂直数量积为零列方程组,求出平面
,利用向量垂直数量积为零列方程组,求出平面![]() 的法向量,平面
的法向量,平面![]() 的法向量为
的法向量为![]() ,由空间向量夹角余弦公式列方程可得结果.
,由空间向量夹角余弦公式列方程可得结果.
详解:(1)取![]() 中点
中点![]() ,连结
,连结![]() ,∵
,∵![]() 分别为
分别为![]() 、
、![]() 中点,∴
中点,∴![]() //
//![]() ,
,![]() , 又点
, 又点![]() 为
为![]() 中点,∴
中点,∴![]() 且
且![]() ,∴四边形
,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ∥
∥![]() ,
,
又![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.
(2)取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,∵
,∵![]()
![]() 是以
是以![]()
![]() 为直角的等腰直角三角形,又
为直角的等腰直角三角形,又![]() 为
为![]() 的中点,∴
的中点,∴![]()
![]()
![]() ,又平面
,又平面![]() ⊥平面
⊥平面![]() ,由面面垂直的性质定理得
,由面面垂直的性质定理得![]() ⊥平面
⊥平面![]() ,又
,又![]()
![]() 平面
平面![]() ,∴
,∴![]() ⊥
⊥![]() ,由已知易得:
,由已知易得:![]() 、
、![]() 、
、![]() 两两垂直. 以
两两垂直. 以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 正方向为x轴、y轴、z轴正方向建立空间直角坐标系如图示,
正方向为x轴、y轴、z轴正方向建立空间直角坐标系如图示,
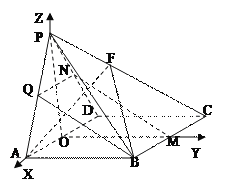
则![]() ,设
,设![]()
![]() ,
,
则:![]() ,
,![]() .
.
设平面ABF的法向量为![]() ,则
,则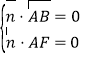 ,
,
∴![]() ,令
,令![]() ,则
,则
![]() ,∴
,∴![]() .
.
又平面![]() 的法向量为
的法向量为![]() ,由二面角
,由二面角![]() 成
成![]() 角得:
角得: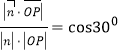 ,
,
∴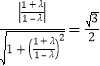 ,解得:
,解得:![]() ,或
,或![]() 不合题意,舍去
不合题意,舍去
.∴![]() ,当棱
,当棱![]() 上的点
上的点![]() 满足
满足![]() 时, 二面角
时, 二面角![]() 成
成![]() 角.
角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】下列命题正确个数为( )
(1)若![]() ,当
,当![]() 时,则
时,则![]() 在
在![]() 上是单调递增函数;
上是单调递增函数;
(2)![]() 单调减区间为
单调减区间为![]() ;
;
(3)
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 4 | 3 | 2 | 1 | -2 | -3 | -4 |
上述表格中的函数是奇函数;
(4)若![]() 是
是![]() 上的偶函数,则
上的偶函数,则![]() 都在
都在![]() 图像上.
图像上.
A.0B.1个C.2个D.3个

