题目内容
8.已知抛物线y2=2px(p>0)的焦点为F,直线y=2x交抛物线于O,A两点,直线AF交抛物线于另一点B,则tan∠AOB=-$\frac{4}{3}$.分析 联立直线方程和抛物线方程,求得A的坐标,由F的坐标,可得B的坐标,再由二倍角的正切公式,计算即可得到所求值.
解答 解:由$\left\{\begin{array}{l}{y=2x}\\{{y}^{2}=2px}\end{array}\right.$,
得A($\frac{1}{2}$p,p),又F($\frac{1}{2}$p,0),
∴B($\frac{1}{2}$p,-p),
∴∠AOB=2∠AOF,tan∠AOF=$\frac{p}{\frac{1}{2}p}$=2,
则 tan∠AOB=$\frac{2tan∠AOF}{1-ta{n}^{2}∠AOF}$=$\frac{2×2}{1-{2}^{2}}$=-$\frac{4}{3}$.
故答案为:-$\frac{4}{3}$.
点评 本题考查直线和抛物线的位置关系,考查二倍角的正切公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
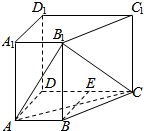 如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.
如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.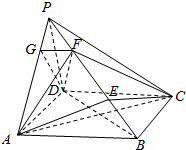 已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2.
已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2. 如图,斜四边形ABCD-A1B1C1D1的底面是边长为8cm的正方形,侧棱AA1成为12cm,且上底面的顶点A1与下底面各点间的距离相等,则四棱柱的侧面积是$32\sqrt{15}$.
如图,斜四边形ABCD-A1B1C1D1的底面是边长为8cm的正方形,侧棱AA1成为12cm,且上底面的顶点A1与下底面各点间的距离相等,则四棱柱的侧面积是$32\sqrt{15}$.