题目内容
【题目】已知函数f(x)=(2x﹣a)2+(2﹣x+a)2 , x∈[﹣1,1].
(1)若设t=2x﹣2﹣x , 求出t的取值范围(只需直接写出结果,不需论证过程);并把f(x)表示为t的函数g(t);
(2)求f(x)的最小值;
(3)关于x的方程f(x)=2a2有解,求实数a的取值范围.
【答案】
(1)解:f(x)=(2x﹣a)2+(2﹣x+a)2=(2x﹣2﹣x)2﹣2a(2x﹣2﹣x)+2a2+2
令t=2x﹣2﹣x,x∈[﹣1,1],∴ ![]()
f(x)表示为t的函数g(t)=t2﹣2at+2a2+2=(t﹣a)2+a2+2
(2)解:g(t)=t2﹣2at+2a2+2=(t﹣a)2+a2+2, ![]()
当 ![]() 时,
时, ![]()
当 ![]() 时,
时, ![]()
当 ![]() 时,
时, ![]() ,
,
∴ 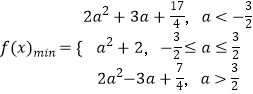
(3)解:方程f(x)=2a2有解,即方程t2﹣2at+2=0在 ![]() 上有解,而t≠0
上有解,而t≠0
∴ ![]() ,
,
令 ![]() ,则
,则 ![]() ,∴函数在
,∴函数在 ![]() 上单调递减,
上单调递减, ![]() 上单调递增
上单调递增
∴ ![]() ,
,
又 ![]() 为奇函数,∴当
为奇函数,∴当 ![]() 时
时 ![]()
∴a的取值范围是 ![]()
【解析】(1)展开,换元,代入可得函数解析式;(2)利用配方法,分类讨论,可求f(x)的最小值;(3)方程f(x)=2a2有解,即方程t2﹣2at+2=0在 ![]() 上有解,分离参数,利用基本不等式可得结论.
上有解,分离参数,利用基本不等式可得结论.
【考点精析】本题主要考查了函数的最值及其几何意义和函数的零点的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点才能正确解答此题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目