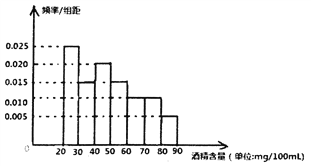
题目内容
【题目】如图，在Rt△AOB中，∠OAB= 
，斜边AB=4．Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B﹣AO﹣C是直二面角，动点D在斜边AB上．
（Ⅰ）求证：平面COD⊥平面AOB；
（Ⅱ）当VA﹣DOC：VA﹣BOC=1：2时，求CD与平面AOB所成角的大小．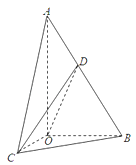
【答案】证明：（Ⅰ）由题意，CO⊥AO，BO⊥AO，
∴∠BOC是二面角B﹣AO﹣C是直二面角，
又∵二面角B﹣AO﹣C是直二面角，∴CO⊥BO，
又∵AO∩BO=O，∴CO⊥平面AOB，
又CO平面COD，∴平面COD⊥平面AOB．
解：（Ⅱ）当VA﹣DOC：VA﹣BOC=1：2时，D为AB中点，
以O为原点，OC为x轴，OB为y轴，OA为z轴，建立空间直角坐标系O﹣xyz，如图，
则B（0，2，0），A（0，0，2 
），C（2，0，0），D（0，1， ），
∴ 
=（﹣2，1， ），
平面AOB的法向量 
=（1，0，0），
设CD与平面AOB所成角为θ，
则sinθ=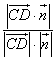 
= 
= 
．
∴θ=45°．
∴CD与平面AOB所成角为45°．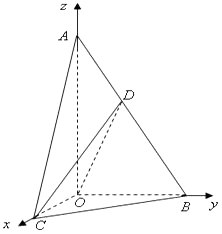
【解析】（Ⅰ）由题意，CO⊥AO，BO⊥AO，∠BOC是二面角B﹣AO﹣C是直二面角，从而CO⊥BO，进而CO⊥平面AOB，由此能证明平面COD⊥平面AOB．（Ⅱ）当VA﹣DOC：VA﹣BOC=1：2时，D为AB中点，以O为原点，OC为x轴，OB为y轴，OA为z轴，建立空间直角坐标系O﹣xyz，利用向量法能求出CD与平面AOB所成角．
【考点精析】根据题目的已知条件，利用平面与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直；已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则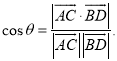
．
