题目内容
(本小题满分12分)
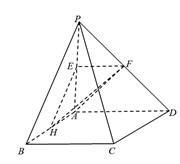
如图,四棱锥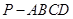 的底面为正方形,侧棱
的底面为正方形,侧棱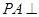 底面
底面 ,且
,且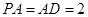 ,
,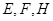 分别是线段
分别是线段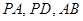 的中点.
的中点.
(Ⅰ)求证: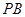 //平面
//平面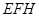 ;
;
(Ⅱ)求证: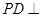 平面
平面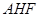 ;
;
(Ⅲ)求二面角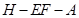 的大小.
的大小.
如图,四棱锥
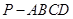 的底面为正方形,侧棱
的底面为正方形,侧棱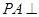 底面
底面 ,且
,且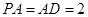 ,
,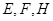 分别是线段
分别是线段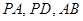 的中点.
的中点.
(Ⅰ)求证:
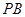 //平面
//平面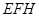 ;
;(Ⅱ)求证:
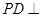 平面
平面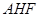 ;
;(Ⅲ)求二面角
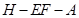 的大小.
的大小.(1)、(2)见解析;(3)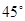
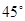
(1)因为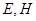 分别是线段
分别是线段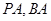 的中点,所以
的中点,所以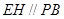 ,由线面平行的判定定理得
,由线面平行的判定定理得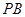 //平面
//平面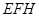 ;(2)由已知易证
;(2)由已知易证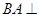 平面
平面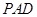 ,所以
,所以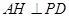 ,又
,又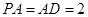 ,
,
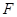 分别是线段
分别是线段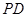 的中点,得
的中点,得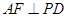 ,根据线面垂直的判定定理得
,根据线面垂直的判定定理得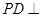 平面
平面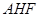 ;(3)由二面角的定义知
;(3)由二面角的定义知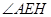 就是所求二面角的平面角,等于
就是所求二面角的平面角,等于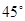 .另解:因为四棱锥
.另解:因为四棱锥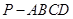 的底面为正方形,侧棱
的底面为正方形,侧棱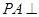 底面
底面 ,可建立空间直角坐标系,写出需要的各点坐标.(1)只需证出
,可建立空间直角坐标系,写出需要的各点坐标.(1)只需证出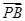 与
与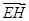 共线;(2)只需证
共线;(2)只需证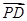 与平面
与平面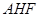 内的任意两个不共线向量垂直;(3)需求出平面
内的任意两个不共线向量垂直;(3)需求出平面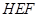 的法向量和平面
的法向量和平面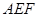 的法向量,把二面角转化为两个法向量的夹角,注意角的范围.
的法向量,把二面角转化为两个法向量的夹角,注意角的范围.
建立如图所示的空间直角坐标系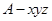 ,
,
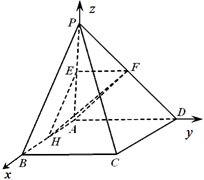
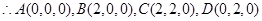 ,
,
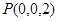 ,
,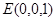 ,
,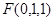 ,
,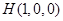 .…………1分
.…………1分
(Ⅰ)证明:
∵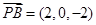 ,
,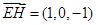 ,
,
∴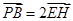 ,
,
∵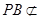 平面
平面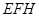 ,且
,且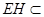 平面
平面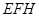 ,
,
∴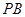 //平面
//平面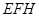 .………………………………4分
.………………………………4分
(Ⅱ)证明:
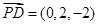 ,
,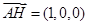 ,
,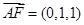 ,
,
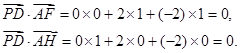
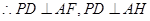 ,
,
又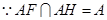 ,
,
∴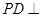 平面
平面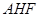 . ………………………………………………8分
. ………………………………………………8分
(Ⅲ)设平面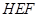 的法向量为
的法向量为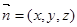 ,
,
因为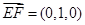 ,
,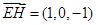 ,
,
则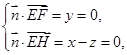 取
取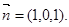
又因为平面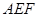 的法向量为
的法向量为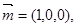
所以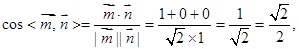
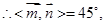
所以二面角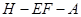 的大小为
的大小为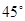 .…………………………………12分
.…………………………………12分
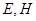 分别是线段
分别是线段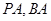 的中点,所以
的中点,所以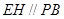 ,由线面平行的判定定理得
,由线面平行的判定定理得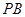 //平面
//平面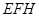 ;(2)由已知易证
;(2)由已知易证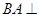 平面
平面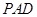 ,所以
,所以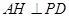 ,又
,又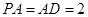 ,
,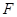 分别是线段
分别是线段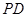 的中点,得
的中点,得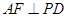 ,根据线面垂直的判定定理得
,根据线面垂直的判定定理得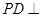 平面
平面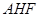 ;(3)由二面角的定义知
;(3)由二面角的定义知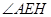 就是所求二面角的平面角,等于
就是所求二面角的平面角,等于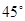 .另解:因为四棱锥
.另解:因为四棱锥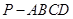 的底面为正方形,侧棱
的底面为正方形,侧棱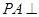 底面
底面 ,可建立空间直角坐标系,写出需要的各点坐标.(1)只需证出
,可建立空间直角坐标系,写出需要的各点坐标.(1)只需证出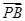 与
与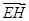 共线;(2)只需证
共线;(2)只需证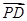 与平面
与平面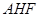 内的任意两个不共线向量垂直;(3)需求出平面
内的任意两个不共线向量垂直;(3)需求出平面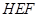 的法向量和平面
的法向量和平面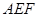 的法向量,把二面角转化为两个法向量的夹角,注意角的范围.
的法向量,把二面角转化为两个法向量的夹角,注意角的范围.建立如图所示的空间直角坐标系
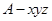 ,
,
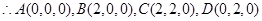 ,
,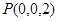 ,
,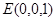 ,
,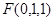 ,
,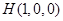 .…………1分
.…………1分(Ⅰ)证明:
∵
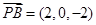 ,
,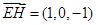 ,
,∴
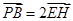 ,
,∵
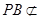 平面
平面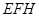 ,且
,且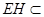 平面
平面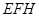 ,
, ∴
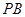 //平面
//平面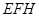 .………………………………4分
.………………………………4分(Ⅱ)证明:
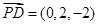 ,
,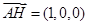 ,
,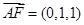 ,
, 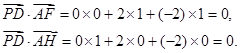
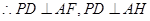 ,
,又
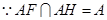 ,
, ∴
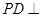 平面
平面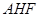 . ………………………………………………8分
. ………………………………………………8分(Ⅲ)设平面
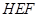 的法向量为
的法向量为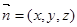 ,
, 因为
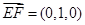 ,
,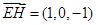 ,
,则
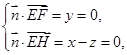 取
取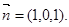
又因为平面
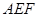 的法向量为
的法向量为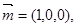
所以
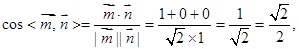
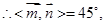
所以二面角
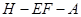 的大小为
的大小为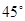 .…………………………………12分
.…………………………………12分
练习册系列答案
相关题目
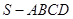 中,
中,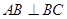 ,
,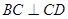 ,侧面
,侧面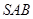 为等边三角形,
为等边三角形,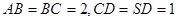 .
.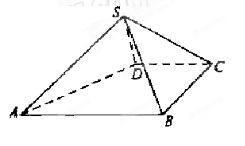
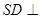 平面
平面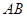 与平面
与平面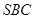 所成角的正弦值.
所成角的正弦值.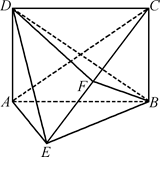
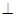 底面ABCD,
底面ABCD,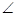 DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.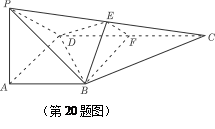
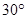 ,求k的取值范围.
,求k的取值范围. 的底面边长为
的底面边长为 ,
, 为
为 中点.
中点.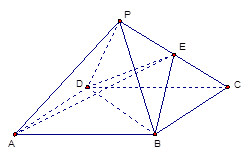
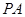 //平面
//平面 ;
; 是二面角
是二面角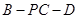 的平面角,求直线
的平面角,求直线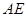 与平面
与平面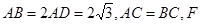 在线段
在线段 上,且
上,且 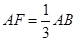 ,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.
,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.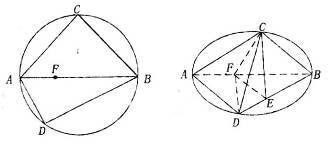
 中,底面
中,底面 是矩形,已知
是矩形,已知 ,
, ,
, ,
, ,
, 。
。 平面
平面 ;
; 的正切值的大小。(12分)
的正切值的大小。(12分)
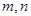 与平面
与平面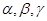 有以下三个命题
有以下三个命题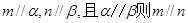
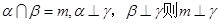
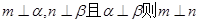 ,其中真命题有
,其中真命题有