题目内容
在四棱锥 中,底面
中,底面 是矩形,已知
是矩形,已知 ,
, ,
, ,
, ,
, 。
。
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的正切值的大小。(12分)
的正切值的大小。(12分)
 中,底面
中,底面 是矩形,已知
是矩形,已知 ,
, ,
, ,
, ,
, 。
。(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的正切值的大小。(12分)
的正切值的大小。(12分)
(1)见解析;(2) .
.
 .
.第一问中,利用线面垂直的判定定理求证。在 中,由题设PA=2,AD=2,
中,由题设PA=2,AD=2,
PD=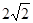 ,可得
,可得 ,于是
,于是
在矩形ABCD中, ,又
,又
 ,从而得到结论。
,从而得到结论。
第二问中,过点P作 于H,过点H作
于H,过点H作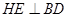 于E,
于E,
连接PE,又因为 平面PAB,
平面PAB,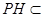 平面PAB,所以
平面PAB,所以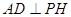 ,
,
又 ,因而
,因而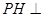 平面ABCD,
平面ABCD,
故HE为PE在平面ABCD内的射影,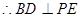 ,从而得到二面角的平面角
,从而得到二面角的平面角 是二面角P-BD-A的平面角,然后借助于三角形求解得到。
是二面角P-BD-A的平面角,然后借助于三角形求解得到。
解:(I)在 中,由题设PA=2,AD=2,
中,由题设PA=2,AD=2,
PD=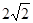 ,可得
,可得 ,
,
于是 ,……….2分,
,……….2分,
在矩形ABCD中, ,又
,又 ….4分,
….4分,
所以 平面PAB。……….6分,
平面PAB。……….6分,
(II)如图所示,过点P作 于H,过点H作
于H,过点H作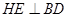 于E,
于E,
连接PE,……….7分,
因为 平面PAB,
平面PAB,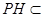 平面PAB,所以
平面PAB,所以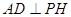 ,
,
又 ,因而
,因而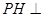 平面ABCD,
平面ABCD,
故HE为PE在平面ABCD内的射影,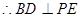 ,……….8分,
,……….8分,
从而 是二面角P-BD-A的平面角。……….9分,
是二面角P-BD-A的平面角。……….9分,
由题设可得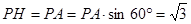 ,
, ,
,
 ,……….10分,
,……….10分,
由 ~
~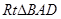 得
得
 ,于是在
,于是在 中,
中,
 ,….11分,
,….11分,
所以二面角P—BD—A 的正切值的大小为 。………….12分
。………….12分
 中,由题设PA=2,AD=2,
中,由题设PA=2,AD=2,PD=
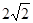 ,可得
,可得 ,于是
,于是在矩形ABCD中,
 ,又
,又
 ,从而得到结论。
,从而得到结论。第二问中,过点P作
 于H,过点H作
于H,过点H作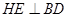 于E,
于E,连接PE,又因为
 平面PAB,
平面PAB,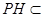 平面PAB,所以
平面PAB,所以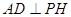 ,
,又
 ,因而
,因而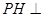 平面ABCD,
平面ABCD,故HE为PE在平面ABCD内的射影,
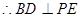 ,从而得到二面角的平面角
,从而得到二面角的平面角 是二面角P-BD-A的平面角,然后借助于三角形求解得到。
是二面角P-BD-A的平面角,然后借助于三角形求解得到。解:(I)在
 中,由题设PA=2,AD=2,
中,由题设PA=2,AD=2,PD=
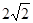 ,可得
,可得 ,
,于是
 ,……….2分,
,……….2分,在矩形ABCD中,
 ,又
,又 ….4分,
….4分,所以
 平面PAB。……….6分,
平面PAB。……….6分,(II)如图所示,过点P作
 于H,过点H作
于H,过点H作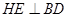 于E,
于E,连接PE,……….7分,
因为
 平面PAB,
平面PAB,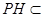 平面PAB,所以
平面PAB,所以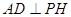 ,
,又
 ,因而
,因而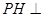 平面ABCD,
平面ABCD,故HE为PE在平面ABCD内的射影,
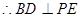 ,……….8分,
,……….8分,从而
 是二面角P-BD-A的平面角。……….9分,
是二面角P-BD-A的平面角。……….9分,由题设可得
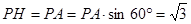 ,
, ,
, ,……….10分,
,……….10分,由
 ~
~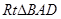 得
得 ,于是在
,于是在 中,
中, ,….11分,
,….11分,所以二面角P—BD—A 的正切值的大小为
 。………….12分
。………….12分
练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
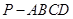 的底面为正方形,侧棱
的底面为正方形,侧棱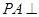 底面
底面 ,且
,且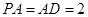 ,
,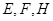 分别是线段
分别是线段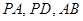 的中点.
的中点.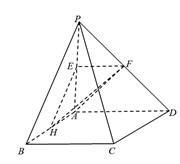
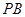 //平面
//平面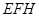 ;
;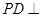 平面
平面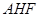 ;
;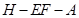 的大小.
的大小.
 与正三角形
与正三角形 所在的平面互相垂直,
所在的平面互相垂直,  、
、 分别为棱
分别为棱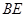 、
、 的中点,
的中点, ,
, ,
, 平面
平面 ;
; 的大小.
的大小.
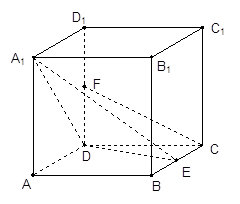
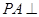 ⊙O,C为圆周上一点,若
⊙O,C为圆周上一点,若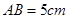 ,
,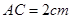 ,则B点到平面PAC的距离为 。
,则B点到平面PAC的距离为 。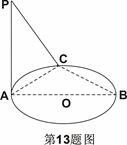




 和直线
和直线 ,具备下列哪一个条件时
,具备下列哪一个条件时 ( )
( ) 


