题目内容
设平面向量a=(cosx,sinx),b=(cosx+2 ,sinx),x∈R.
,sinx),x∈R.
(1)若x∈(0, ),证明:a和b不平行;
),证明:a和b不平行;
(2)若c=(0,1),求函数f(x)=a·(b-2c)的最大值,并求出相应的x值.
(1)见解析 (2) f(x)max=5,x=2kπ-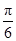 (k∈Z)
(k∈Z)
解析(1)证明:假设a与b平行,
则cosxsinx-sinx(cosx+2 )=0,
)=0,
即sinx=0,与x∈(0, )时,sinx>0,矛盾.
)时,sinx>0,矛盾.
故a与b不平行.
(2)解:f(x)=a·b-2a·c
=cos2x+2 cosx+sin2x-2sinx
cosx+sin2x-2sinx
=1-2sinx+2 cosx
cosx
=1-4sin(x- ).
).
所以f(x)max=5,x=2kπ-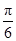 (k∈Z).
(k∈Z).

练习册系列答案
相关题目
 的内角
的内角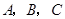 所对的边长分别为
所对的边长分别为 ,且
,且 ,A=
,A= ,
,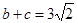 .
.
 的单调递增区间及最大值;
的单调递增区间及最大值;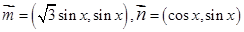 ,函数
,函数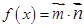 .
.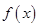 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;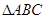 中,角
中,角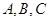 的对边分别为
的对边分别为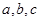 ,若
,若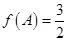 ,
,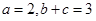 ,
,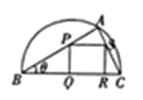
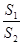 取得最小值时θ的值.
取得最小值时θ的值. )(其中A>0,ω>0,-π<
)(其中A>0,ω>0,-π<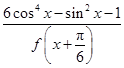 的值域.
的值域.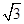 sinx,sinx),b=(cosx,sinx),x∈
sinx,sinx),b=(cosx,sinx),x∈ .
. )的周期为π,且图象上一个最低点为M
)的周期为π,且图象上一个最低点为M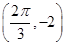 .
. 时,求f(x)的最值.
时,求f(x)的最值.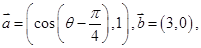 其中
其中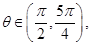 若
若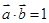 .
.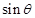 的值;
的值;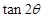 的值.
的值. cos
cos
 ,α∈(0,π),求α的值;
,α∈(0,π),求α的值; 上最大值和最小值.
上最大值和最小值.