题目内容
设函数f(x)=Asin(ωx+ )(其中A>0,ω>0,-π<
)(其中A>0,ω>0,-π< ≤π)在x=
≤π)在x=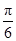 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为 .
.
(1)求f(x)的解析式;
(2)求函数g(x)=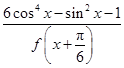 的值域.
的值域.
(1) f(x)=2sin(2x+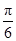 ) (2) [1,
) (2) [1, 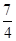 ]∪(
]∪(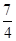 ,
,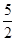 ]
]
解析解:(1)由题设条件知f(x)的周期T=π,
即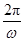 =π,解得ω=2.
=π,解得ω=2.
因为f(x)在x=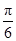 处取得最大值2,所以A=2,
处取得最大值2,所以A=2,
从而sin(2×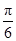 +
+ )=1,
)=1,
所以2×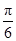 +
+ =
= +2kπ,k∈Z.
+2kπ,k∈Z.
又由-π< ≤π,得
≤π,得 =
=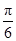 .
.
故f(x)的解析式为f(x)=2sin(2x+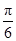 ).
).
(2)g(x)=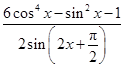
=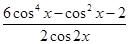
=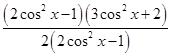
=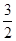 cos2x+1(cos2x≠
cos2x+1(cos2x≠ ).
).
因为cos2x∈[0,1],且cos2x≠ ,
,
故g(x)的值域为[1,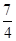 ]∪(
]∪(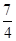 ,
,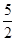 ].
].

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 .
. 的最大值,并写出
的最大值,并写出 的取值集合;
的取值集合; 中,角
中,角 的对边分别为
的对边分别为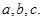 若
若
 求实数
求实数 的最小值.
的最小值.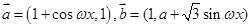 (
(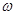 为常数且
为常数且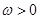 ),函数
),函数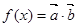 在
在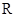 上的最大值为
上的最大值为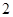 .
.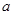 的值;
的值;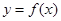 的图象向右平移
的图象向右平移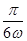 个单位,可得函数
个单位,可得函数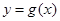 的图象,若
的图象,若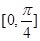 上为增函数,求
上为增函数,求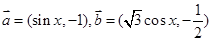 ,函数
,函数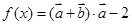 求函数
求函数 的最小正周期T及值域
的最小正周期T及值域 .
. 的最小正周期;
的最小正周期; 时,求函数
时,求函数 ,sinx),x∈R.
,sinx),x∈R.
 +1)x+m=0的两根为sinθ和cosθ,且θ∈(0,2π).
+1)x+m=0的两根为sinθ和cosθ,且θ∈(0,2π). 的值;
的值;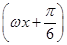 +
+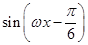 -2cos2
-2cos2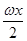 ,x∈R(其中ω>0).
,x∈R(其中ω>0). ,求函数y=f(x)的单调增区间.
,求函数y=f(x)的单调增区间.