题目内容
如图所示,在直径为BC的半圆中,A是弧BC上一点,正方形PQRS内接于△ABC,若BC=a,∠ABC=θ,设△ABC的面积为Sl,正方形PQRS的面积为S2.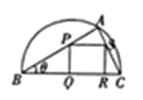
(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求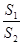 取得最小值时θ的值.
取得最小值时θ的值.
(1) ,
,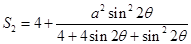 ;(2)
;(2)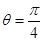 .
.
解析试题分析:本题主要以圆为几何背景考查三角函数的定义、三角函数的面积公式、函数的单调性及最值等数学知识,考查学生的分析问题的能力、转化能力和计算能力.第一问,在 中,求出
中,求出 ,利用
,利用 求
求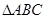 的面积,在
的面积,在 中求出
中求出 ,在
,在 中求出
中求出 ,而
,而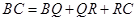 ,求出x的值,再求正方形PQRS的面积
,求出x的值,再求正方形PQRS的面积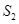 ;第二问,先将第一问的结论代入
;第二问,先将第一问的结论代入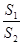 中化简表达式,用换元法,简化表达式,利用函数
中化简表达式,用换元法,简化表达式,利用函数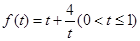 的单调性求
的单调性求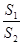 的最小值.
的最小值.
试题解析:(1)因为AB=acosθ,
∴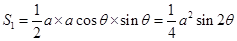 ,
,
设正方形边长为x,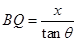 ,RC=xtanθ,
,RC=xtanθ,
则 ,解之得
,解之得
所以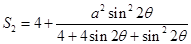 (6分)
(6分)
(2)当a固定,θ变化时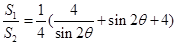 ,
,
设sin2θ=t,则 .
.
∵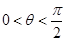 ,∴0<t≤1,
,∴0<t≤1,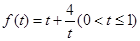 ,
,
易证f(t)在(0,1]上是减函数.
故当t=1时,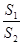 取最小值,此时
取最小值,此时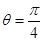 (12分)
(12分)
考点:1.三角函数的定义;2.三角形面积公式;3.函数的单调性.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 ,其中
,其中 为常数.
为常数. 的周期;
的周期; 的最小值为
的最小值为 ,求
,求 的最大值及图像的对称轴方程.
的最大值及图像的对称轴方程. 的部分图像如图所示.
的部分图像如图所示.
 的内角分别是A,B,C.若f(A)=1,
的内角分别是A,B,C.若f(A)=1,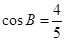 ,求sinC的值.
,求sinC的值. (
( )的最小正周期为
)的最小正周期为 .
. 的单调增区间;
的单调增区间; 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图象;若
的图象;若 上至少含有10个零点,求b的最小值.
上至少含有10个零点,求b的最小值.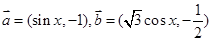 ,函数
,函数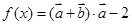 求函数
求函数 的最小正周期T及值域
的最小正周期T及值域 ),b=(
),b=( sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b. ]上的最大值和最小值.
]上的最大值和最小值.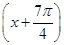 +cos
+cos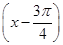 ,x∈R.
,x∈R.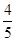 ,cos(β+α)=-
,cos(β+α)=-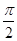 ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0. cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+ .
. 时,求函数f(x)的值域;
时,求函数f(x)的值域; 的值;
的值; 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.