题目内容
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,且
,且![]() (如图①).将四边形
(如图①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() 、
、![]() 、
、![]() (如图②).在折起的过程中,则下列表述:
(如图②).在折起的过程中,则下列表述:

①![]() 平面
平面![]() ;
;
②四点![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.其中正确的是__________.
可能垂直.其中正确的是__________.
【答案】①③
【解析】
连接![]() 、
、![]() 交于点
交于点![]() ,取
,取![]() 的中点
的中点![]() ,证明四边形
,证明四边形![]() 为平行四边形,可判断命题①的正误;利用线面平行的性质定理和空间平行线的传递性可判断命题②的正误;连接
为平行四边形,可判断命题①的正误;利用线面平行的性质定理和空间平行线的传递性可判断命题②的正误;连接![]() ,证明出
,证明出![]() ,结合线面垂直和面面垂直的判定定理可判断命题③的正误;假设平面
,结合线面垂直和面面垂直的判定定理可判断命题③的正误;假设平面![]() 与平面
与平面![]() 垂直,利用面面垂直的性质定理可判断命题④的正误.综合可得出结论.
垂直,利用面面垂直的性质定理可判断命题④的正误.综合可得出结论.
对于命题①,连接![]() 、
、![]() 交于点
交于点![]() ,取
,取![]() 的中点
的中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,如下图所示:
,如下图所示:
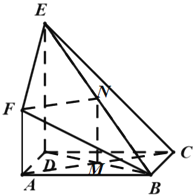
则![]() 且
且![]() ,四边形
,四边形![]() 是矩形,且
是矩形,且![]() ,
,![]() 为
为![]() 的中点,
的中点,
![]() 为
为![]() 的中点,
的中点,![]() 且
且![]() ,
,![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,即
,即![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,命题①正确;
,命题①正确;
对于命题②,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
若四点![]() 、
、![]() 、
、![]() 、
、![]() 共面,则这四点可确定平面
共面,则这四点可确定平面![]() ,则
,则![]() ,平面
,平面![]() 平面
平面![]() ,由线面平行的性质定理可得
,由线面平行的性质定理可得![]() ,
,
则![]() ,但四边形
,但四边形![]() 为梯形且
为梯形且![]() 、
、![]() 为两腰,
为两腰,![]() 与
与![]() 相交,矛盾.
相交,矛盾.
所以,命题②错误;
对于命题③,连接![]() 、
、![]() ,设
,设![]() ,则
,则![]() ,
,
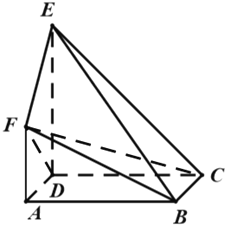
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 为等腰直角三角形,
为等腰直角三角形,
且![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
由余弦定理得![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() 、
、![]() 为平面
为平面![]() 内的两条相交直线,所以,
内的两条相交直线,所以,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,命题③正确;
,命题③正确;
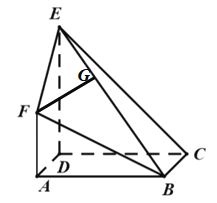
对于命题④,假设平面![]() 与平面
与平面![]() 垂直,过点
垂直,过点![]() 在平面
在平面![]() 内作
内作![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
![]() ,
,![]() ,显然
,显然![]() 与
与![]() 不垂直,命题④错误.
不垂直,命题④错误.
故答案为:①③.

练习册系列答案
相关题目