题目内容
【题目】设![]() 是平面内共始点的三个非零向量,且两两不共线,
是平面内共始点的三个非零向量,且两两不共线,![]() 有下列命题:
有下列命题:
(1)关于![]() 的方程
的方程![]() 可能有两个不同的实数解;
可能有两个不同的实数解;
(2)关于![]() 的方程
的方程![]() 至少有一个实数解;
至少有一个实数解;
(3)关于![]() 的方程
的方程![]() 最多有一个实数解;
最多有一个实数解;
(4)关于![]() 的方程
的方程![]() 若有实数解,则三个向量的终点不可能共线;
若有实数解,则三个向量的终点不可能共线;
上述命题正确的序号是__________
【答案】(3)(4)
【解析】
关于![]() 的方程
的方程![]() ,对
,对![]() ,以
,以![]() 作为一组基底表示平面内的向量,利用平面向量基本定理讨论解的个数.
作为一组基底表示平面内的向量,利用平面向量基本定理讨论解的个数.
![]() 是平面内共始点的三个非零向量,且两两不共线,
是平面内共始点的三个非零向量,且两两不共线,![]() ,以
,以![]() 作为一组基底,
作为一组基底,
则任意向量![]() 存在唯一的有序数对
存在唯一的有序数对![]() 使
使![]() ,
,
关于![]() 的方程
的方程![]() ,即
,即![]() ,即
,即![]() ,
,
![]() 与
与![]() 一一对应,所以不可能两个实数解,故命题(1)错误;
一一对应,所以不可能两个实数解,故命题(1)错误;
若![]() ,无解,故命题(2)错误;
,无解,故命题(2)错误;
当![]() 时,方程有解,结合(1),方程最多一个解所以(3)正确;
时,方程有解,结合(1),方程最多一个解所以(3)正确;
根据平面向量共线定理,平面内有三个不同点![]() 共线,O为坐标原点,必存在实数
共线,O为坐标原点,必存在实数![]() 使:
使:![]() ,
,
即![]() ,
,
整理得:![]() ,
,
即三个向量![]() 的终点共线,
的终点共线,![]() ,必有
,必有![]() ,与
,与![]() 矛盾,所以三个向量终点不可能共线,故(4)正确.
矛盾,所以三个向量终点不可能共线,故(4)正确.
故答案为:(3)(4)

【题目】某市高中某学科竞赛中,某区![]() 名考生的参赛成绩的频率分布直方图如图所示.
名考生的参赛成绩的频率分布直方图如图所示.
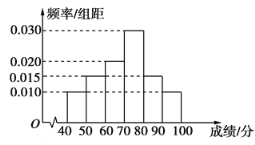
(1)求这![]() 名考生的平均成绩
名考生的平均成绩![]() (同一组中数据用该组区间中点值作代表);
(同一组中数据用该组区间中点值作代表);
(2)记![]() 分以上为合格,
分以上为合格,![]() 分及以下为不合格,结合频率分布直方图完成下表,能否在犯错误概率不超过
分及以下为不合格,结合频率分布直方图完成下表,能否在犯错误概率不超过![]() 的前提下认为该学科竞赛成绩与性别有关?
的前提下认为该学科竞赛成绩与性别有关?
不合格 | 合格 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
附:
|
|
|
|
|
|
|
|
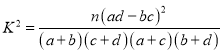 .
.
【题目】在某区“创文明城区”(简称“创城”)活动中,教委对本区![]() 四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
学校 |
|
|
|
|
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
(注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值)假设每名高中学生是否参与”创城”活动是相互独立的.
(1)若该区共2000名高中学生,估计![]() 学校参与“创城”活动的人数;
学校参与“创城”活动的人数;
(2)在随机抽查的100名高中学生中,随机抽取1名学生,求恰好该生没有参与“创城”活动的概率;
(3)在上表中从![]() 两校没有参与“创城”活动的同学中随机抽取2人,求恰好
两校没有参与“创城”活动的同学中随机抽取2人,求恰好![]() 两校各有1人没有参与“创城”活动的概率是多少?
两校各有1人没有参与“创城”活动的概率是多少?