题目内容
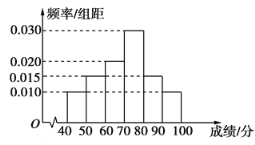
【题目】某市高中某学科竞赛中，某区
名考生的参赛成绩的频率分布直方图如图所示．
（1）求这名考生的平均成绩
（同一组中数据用该组区间中点值作代表）；
（2）记
分以上为合格，分及以下为不合格，结合频率分布直方图完成下表，能否在犯错误概率不超过
的前提下认为该学科竞赛成绩与性别有关？
不合格 | 合格 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
附：
|
|
|
|
|
|
|
|
.
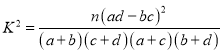【答案】（1）
；（2）填表见解析，能在犯错误概率不超过
的前提下认为该学科竞赛成绩与性别有关.
【解析】
（1）将每个矩形底边中点值乘以相应矩形的面积，相加即可得出这
名考生的平均成绩
；
（2）根据题中信息完善
列联表，并计算出
的观测值，利用临界值表可对题中结论进行判断.
（1）由题意，得：
中间值 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
（分），
这名考生的平均成绩为
分；
（2）列联表如下：
不合格 | 合格 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
，
故能在犯错误概率不超过的前提下认为该学科竞赛成绩与性别有关．
练习册系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
【题目】为了解人们对“延迟退休年龄政策”的态度，某部门从年龄在15岁到65岁的人群中随机调查了100人，并得到如图所示的频率分布直方图，在这100人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如表所示：
(1)由频率分布直方图，估计这100人年龄的平均数；
(2)根据以上统计数据填写下面的2
2列联表，据此表，能否在犯错误的概率不超过5%的前提下，认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异？
45岁以下 | 45岁以上 | 总计 | |
不支持 | |||
支持 | |||
总计 |
参考数据：
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
