题目内容
16.设z∈C,则方程|z+3|+|z-3|=8对应曲线的普通方程是$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}=1$.分析 设z=x+yi(x,y∈R),代入|z+3|+|z-3|=8,整理即可求得方程|z+3|+|z-3|=8对应曲线的普通方程.
解答 解:设z=x+yi(x,y∈R),
由|z+3|+|z-3|=8,得
$\sqrt{(x+3)^{2}+{y}^{2}}+\sqrt{(x-3)^{2}+{y}^{2}}=8$,整理得:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}=1$.
∴方程|z+3|+|z-3|=8对应曲线的普通方程是:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}=1$.
故答案为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}=1$.
点评 本题考查了复数的代数表示法及其几何意义,考查了轨迹方程的求法,是基础题.

练习册系列答案
相关题目
7.已知曲线y=f(x)在点(1,f(1))处的切线方程为2x-y+2=0,则f′(1)=( )
| A. | 4 | B. | -4 | C. | -2 | D. | 2 |
1.已知函数f(x)=sin$\frac{πx}{3}$,则f(1)+f(2)+…+f(2015)=( )
| A. | 2015 | B. | 1 | C. | -1 | D. | 0 |
 在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,BD⊥DC,侧面PAB⊥底面ABCD,PA=AD=AB,点M是PB的中点.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,BD⊥DC,侧面PAB⊥底面ABCD,PA=AD=AB,点M是PB的中点.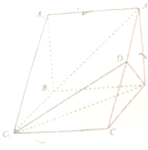 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点.