若实数x.y满足条件$\left\{\begin{array}{l}{y≥2|x|-1}\\{y≤x+1}\end{array}\right.$.则z=x+3y的最小值为-3．题目和参考答案——青夏教育精英家教网—

题目内容

5．若实数x，y满足条件$\left\{\begin{array}{l}{y≥2|x|-1}\\{y≤x+1}\end{array}\right.$，则z=x+3y的最小值为-3．

分析作出不等式组对应的平面区域，利用z的几何意义即可得到结论．

解答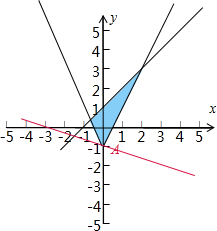解：作出不等式组$\left\{\begin{array}{l}y≥2|x|-1\\ y≤x+1\end{array}\right.$对应的平面区域，
由z=x+3y，得y=-$\frac{1}{3}$x+$\frac{z}{3}$，平移直线y=-$\frac{1}{3}$x+$\frac{z}{3}$，
由图象可知当直线经过点A时，
直线y=-$\frac{1}{3}$x+$\frac{z}{3}$的截距最小，此时z最小，
由$\left\{\begin{array}{l}y=2x-1\\ y=-2x-1\end{array}\right.$，得$\left\{\begin{array}{l}x=0\\ y=-1\end{array}\right.$，即A（0，-1）
此时z=0+3×（-1）=-3．
故答案为：-3．

点评本题主要考查线性规划的应用，利用数形结合是解决本题的关键．

练习册系列答案

16．设z∈C，则方程|z+3|+|z-3|=8对应曲线的普通方程是$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}=1$．

13．函数f（x）=3sin（2x+φ）（0＜φ＜π）的图象向右平移$\frac{π}{3}$个单位后关于y轴对称，则f（x）的单调增区间为（　　）

	A．	[-$\frac{π}{4}$+kπ，$\frac{π}{4}$+kπ]，k∈Z		B．	[-$\frac{π}{6}$+kπ，$\frac{π}{3}$+kπ]，k∈Z
	C．	[-$\frac{π}{3}$+kπ，$\frac{π}{6}$+kπ]，k∈Z		D．	[kπ，$\frac{π}{2}$+kπ]，k∈Z