题目内容
20.若不等式-4<2x-3<4与不等式x2+px+q<0的解集相同,则$\frac{p}{q}$=$\frac{12}{7}$.分析 根据题意不等式x2+px+q<0的解集为(-$\frac{1}{2}$,$\frac{7}{2}$),x2+px+q=0的解为x=-$\frac{1}{2}$,或$\frac{7}{2}$,从而可以求得p与q的值,问题得以解决.
解答 解:∵-4<2x-3<4,
∴$-\frac{1}{2}$<x<$\frac{7}{2}$,
∴不等式-4<2x-3<4的解集为(-$\frac{1}{2}$,$\frac{7}{2}$),
∴x2+px+q=0的解为x=-$\frac{1}{2}$,或$\frac{7}{2}$,
结合根与系数的关系-$\frac{1}{2}$+$\frac{7}{2}$=3=-p,即p=-3,
-$\frac{1}{2}$×$\frac{7}{2}$=q=,即q=-$\frac{7}{4}$,
∴$\frac{p}{q}$=$\frac{-3}{-\frac{7}{4}}$=$\frac{12}{7}$,
故答案为:$\frac{12}{7}$.
点评 本题给出一元二次不等式的解集,求参数的取值,着重考查了一元二次不等式的解法和根与系数的关系等知识点,属于基础题

练习册系列答案
相关题目
11.如图是一个四棱锥的三视图,则该几何体的体积为( )
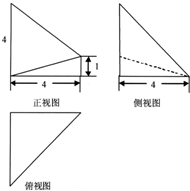

| A. | $\frac{40}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{28}{3}$ |