题目内容
11．如图是一个四棱锥的三视图，则该几何体的体积为（ ）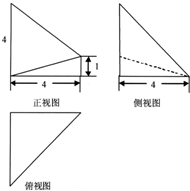
| A． | $\frac{40}{3}$ | B． | $\frac{32}{3}$ | C． | $\frac{16}{3}$ | D． | $\frac{28}{3}$ |
分析 根据几何体的三视图，得出该几何体是底面为直角梯形的直四棱锥，结合图中数据求出它的体积．
解答 
解：根据几何体的三视图，得
该几何体是如图所示的直四棱锥；
且四棱锥的底面为梯形，梯形的上底长为1，下底长为4，高为4；
所以，该四棱锥的体积为
V=S底面积•h=$\frac{1}{3}×[\frac{1}{2}（1+4）×4]×4=\frac{40}{3}$．
故选：A．
点评 本题考查了利用空间几何体的三视图求体积的应用问题，是基础题目．
练习册系列答案
相关题目
2．设f（x）=$\frac{1}{1-x}$，则f[f（x）]的表达式为（ ）
| A． | $\frac{1-x}{x}$ | B． | $\frac{1}{{{{（1-x）}^2}}}$ | C． | 1-$\frac{1}{x}$ | D． | $\frac{1}{1-x}$ |
6．空间向量不可以做的运算是（ ）
| A． | 加法 | B． | 减法 | C． | 数量积 | D． | 除法 |
16．
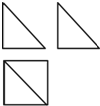利用一球体毛坯切削后得到一个几何体，该几何体的三视图如图所示，若主视图和左视图都是直角边长为1的等腰直角三角形，则毛坯球体的体积最小应为（ ）
利用一球体毛坯切削后得到一个几何体，该几何体的三视图如图所示，若主视图和左视图都是直角边长为1的等腰直角三角形，则毛坯球体的体积最小应为（ ）| A． | $\frac{{\sqrt{2}π}}{3}$ | B． | $\frac{4π}{3}$ | C． | $\frac{\sqrt{3}π}{2}$ | D． | $\frac{8\sqrt{2}π}{3}$ |