题目内容
3.设直线nx+(n+1)y=$\sqrt{2}(n∈{N^*})$与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…S2013的值为( )| A. | $\frac{2014}{2015}$ | B. | $\frac{2011}{2012}$ | C. | $\frac{2012}{2013}$ | D. | $\frac{2013}{2014}$ |
分析 直线nx+(n+1)y=$\sqrt{2}(n∈{N^*})$,可得与坐标轴的交点分别为:$(\frac{\sqrt{2}}{n},0)$,$(0,\frac{\sqrt{2}}{n+1})$,于是直线与两坐标轴围成的三角形面积为Sn=$\frac{1}{n}-\frac{1}{n+1}$.利用“裂项求和”即可得出.
解答 解:∵直线nx+(n+1)y=$\sqrt{2}(n∈{N^*})$,
∴与坐标轴的交点分别为:$(\frac{\sqrt{2}}{n},0)$,$(0,\frac{\sqrt{2}}{n+1})$,
∴直线与两坐标轴围成的三角形面积为Sn=$\frac{1}{2}×\frac{\sqrt{2}}{n}×\frac{\sqrt{2}}{n+1}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
则S1+S2+S3+…S2013的值=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{2013}-\frac{1}{2014})$
=1-$\frac{1}{2014}$
=$\frac{2013}{2014}$.
故选:D.
点评 本题考查了直线的截距式、三角形的面积计算公式、“裂项求和”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.点A,B,C,D在格点图的位置如图所示,则向量$\overrightarrow{AD}$+$\overrightarrow{AC}$在$\overrightarrow{AB}$方向上的投影为( )
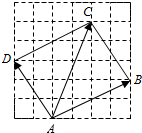

| A. | -$\frac{\sqrt{5}}{5}$ | B. | -$\frac{8\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | 2 |
18.复数Z=i+1共轭复数的虚部是( )
| A. | -1 | B. | 1 | C. | i | D. | -i |
15.设实数x,y满足$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$,则$\frac{x+3}{y+1}$的取值范围是( )
| A. | [$\frac{5}{7}$,5] | B. | [$\frac{5}{7}$,1] | C. | [$\frac{1}{5}$,$\frac{7}{5}$] | D. | (-∞,$\frac{1}{5}$]∪[$\frac{7}{5}$,+∞) |