题目内容
13.在△ABC中,3sinA=4sinB=6sinC,则cosB=$\frac{11}{16}$.分析 由正弦定理可得3sinA=4sinB=6sinC,进而可用a表示b,c,代入余弦定理化简可得.
解答 解:∵3sinA=4sinB=6sinC,
∴由正弦定理可得3a=4b=6c
∴b=$\frac{3a}{4}$,c=$\frac{1}{2}$a,
由余弦定理可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+\frac{{a}^{2}}{4}-\frac{9{a}^{2}}{16}}{2×a×\frac{1}{2}a}$=$\frac{11}{16}$.
故答案为:$\frac{11}{16}$.
点评 本题考查正余弦定理的应用,用a表示b,c是解决问题的关键,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.设直线nx+(n+1)y=$\sqrt{2}(n∈{N^*})$与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…S2013的值为( )
| A. | $\frac{2014}{2015}$ | B. | $\frac{2011}{2012}$ | C. | $\frac{2012}{2013}$ | D. | $\frac{2013}{2014}$ |
4.设p:“lgx,lg(x+1),lg(x+3)成等差数列”,q:“2x+1-$\frac{8}{3},{2^x}$,3成等比数列”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
1.设$\overrightarrow{a}$、$\overrightarrow{b}$是两个单位向量,其夹角为θ,则“$\frac{π}{6}<θ<\frac{π}{3}$”是“|$\overrightarrow{a}$-$\overrightarrow{b}$|<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.已知函数y=f(x)的反函数f-1(x)=log${\;}_{\frac{1}{2}}$x,则方程 f(x)=1的解集是( )
| A. | {1} | B. | {2} | C. | {3} | D. | {0} |
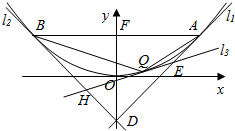 如图,已知抛物线C:x2=2py(p>0),其焦点F到准线的距离为2,点A、点B是抛物线C上的定点,它们到焦点F的距离均为2,且点A位于第一象限.
如图,已知抛物线C:x2=2py(p>0),其焦点F到准线的距离为2,点A、点B是抛物线C上的定点,它们到焦点F的距离均为2,且点A位于第一象限.