题目内容
14.已知函数f(x)=$\frac{p{x}^{2}+2}{3x+q}$是奇函数,且f(2)=$\frac{5}{3}$.(1)求实数p,q的值;
(2)判断并证明f(x)在(1,+∞)上的单调性.
(3)求f(x)的值域.
分析 (1)直接根据奇函数的定义确定有关参数的值;
(2)借助于导数求解函数的单调增区间和减区间.
(3)判断函数的极值和单调性,即可得到结论.
解答 解:(1)∵f(x)为奇函数,
∴f(-x)=-f(x),
∴$\frac{p+2}{-3x+q}$=-$\frac{p+2}{3x+q}$,
即-3x+q=-3x-q,
∴q=0,
∵f(2)=$\frac{5}{3}$,
∴$\frac{4p+2}{3×2}$=$\frac{5}{3}$,即4p=8,
∴p=2,
∴实数p,q的值分别为2,0;
(2)f(x)=$\frac{2{x}^{2}+2}{x}$=2x+$\frac{2}{x}$=2(x+$\frac{1}{x}$),
则f′(x)=2(1-$\frac{1}{{x}^{2}}$)=$\frac{2({x}^{2}-1)}{{x}^{2}}$,
令f′(x)>0得x<-1或x>1,令f′(x)<0得-1<x<1,因为x≠0,
所以f(x)的增区间为(-∞,-1),(1,+∞)
减区间为(-1,0),(0,1).
(3)由(2)知,当x>0时,f(x)>0,且当x=1时,函数取得极小值f(1)=4,此时f(x)≥4,
当x<0时,f(x)<0,且当x=-1时,函数取得极大值f(-1)=-4,此时f(x)≤-4,
综上f(x)≥4,或f(x)≤-4,
即函数的值域为(-∞,-4]∪[4,+∞)
点评 本题重点考查了函数是奇函数的重要性质,利用导数研究函数的单调性问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列求导运算正确的是( )
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{x^2}$ | B. | (log3x)′=$\frac{1}{xln3}$ | C. | (5x)′=5xlog5e | D. | (x2cosx)′=2xsinx |
9.设函数$f(x)=\left\{\begin{array}{l}{x^2}+1,x≤1\\ \frac{2}{x},x>1\end{array}\right.$则f(f(4))=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{5}{4}$ |
3.设直线nx+(n+1)y=$\sqrt{2}(n∈{N^*})$与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…S2013的值为( )
| A. | $\frac{2014}{2015}$ | B. | $\frac{2011}{2012}$ | C. | $\frac{2012}{2013}$ | D. | $\frac{2013}{2014}$ |
4.设p:“lgx,lg(x+1),lg(x+3)成等差数列”,q:“2x+1-$\frac{8}{3},{2^x}$,3成等比数列”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
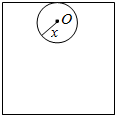 如图,半径为r的圆O在边长为4的正方形内与正方形一边相切并滚动一周后,圆O没有通过区域的面积为S.
如图,半径为r的圆O在边长为4的正方形内与正方形一边相切并滚动一周后,圆O没有通过区域的面积为S.