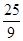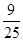题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c.己知(b-2a)cosC+ccosB=0.
(1)求C;
(2)若c=
,b=3a,求△ABC的面积.
(1)求C;
(2)若c=
| 7 |
(1)∵(b-2a)cosC+ccosB=0,
∴由正弦定理得(sinB-2sinA)cosC+sinCcosB=0,
sinBcosC+cosBsinC=2sinAcosC,即sin(B+C)=2sinAcosC,
∴sinA=2sinAcosC,
∵sinA≠0,∴cosC=
,
又∵C∈(0,π),∴C=
;
(2)由余弦定理得:c2=a2+b2-2abcosC,
∴
解得:a=1,b=3,
∴△ABC的面积S=
absinC=
×1×3×
=
.
∴由正弦定理得(sinB-2sinA)cosC+sinCcosB=0,
sinBcosC+cosBsinC=2sinAcosC,即sin(B+C)=2sinAcosC,
∴sinA=2sinAcosC,
∵sinA≠0,∴cosC=
| 1 |
| 2 |
又∵C∈(0,π),∴C=
| π |
| 3 |
(2)由余弦定理得:c2=a2+b2-2abcosC,
∴
|
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
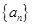 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项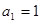 ,
,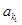 、
、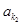 、 、
、 、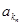 恰为等比数列,且
恰为等比数列,且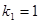 ,
,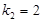 ,
,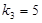 .
.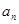 ;
;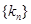 的前
的前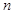 项和为
项和为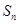 ,求
,求 中,若
中,若 则
则 .
.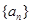 的前n项和为
的前n项和为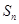 ,若
,若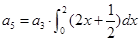 ,则
,则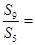 ( ).
( ).