Question

【题目】已知函数，其中a∈R．

（Ⅰ）讨论函数的单调性；

（Ⅱ）当 时，设、为曲线上任意两点，曲线在点处的切线斜率为k，证明：．

Answer 1

【答案】（Ⅰ）当时，的增区间为；当时，在为增函数，在为减函数．（Ⅱ）详见解析．

【解析】

（1）分和两种情况分别讨论导数的符号可得函数的单调区间．

（2）原不等式等价于，不妨设，则不等式又可以转化为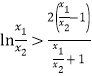即，利用导数可证该不等式．

（1）

当时，，故的增区间为．

当时，

若，则，故在为增函数；

若，则，故在为减函数；

综上，当时，的增区间为；

当时，在为增函数，在为减函数．

（2）当时，，．

原不等式等价于，

不妨设，则原不等式又等价于，该式可进一步化为：

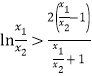，因此原不等式等价于，下证该不等式成立．

令，则，

故在为增函数，所以即成立，

综上，原不等式成立．