题目内容
【题目】已知两点
，
，给出下列曲线方程：（1）
；（2）
；（3）
；（4）
，在曲线上存在点
满足
的所有曲线是（ ）
A.（1）（2）（3）（4）B.（2）（3）
C.（1）（4）D.（2）（3）（4）
【答案】B
【解析】
求出线段MN的垂直平分线方程，然后分别和题目给出的四条曲线方程联立，利用判别式判断直线和曲线的交点情况，从而判断给出的曲线上是否存在点P，使得||PA|＝|PB|．
由A（1，
），B（﹣4，
），
得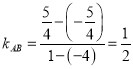
，A、B的中点坐标为（
，0），
∴AB的垂直平分线方程为y﹣0＝﹣2（x
），即y＝﹣2x﹣3．
（1）∵直线y＝﹣2x﹣3与直线4x+2y﹣1＝0平行，
∴直线4x+2y﹣1＝0上不存在点P，使|PA|＝|PB|；
（2）联立
，得5x2+12x+6＝0，△＝122﹣4×5×6＝24＞0．
∴直线y＝﹣2x﹣3与x2+y2＝3有交点，曲线x2+y2＝3上存在点P满足|PA|＝|PB|；
（3）联立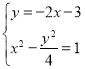
，得
，方程有解，
∴直线y＝﹣2x﹣3与x2
1有交点，曲线x21上存在点P满足|PA|＝|PB|；
（4）联立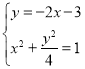
，得8x2+12x+5＝0，△＝122﹣4×8×5＝﹣16＜0．
∴直线y＝﹣2x﹣3与x2
1没有交点，曲线x21上不存在点P满足|PA|＝|PB|．
∴曲线上存在点P满足|PA|＝|PB|的所有曲线是（2）（3）．
故选：B．
练习册系列答案
相关题目
