题目内容
18．已知向量$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（-3，4），则$\overrightarrow{a}$+$\overrightarrow{b}$=（ ）| A． | （-1，5） | B． | （1，5） | C． | （-1，-3） | D． | （1，3） |
分析 直接利用向量的加法运算法则求解即可．
解答 解：向量$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（-3，4），则$\overrightarrow{a}$+$\overrightarrow{b}$=（-1，5）．
故选：A．
点评 本题考查向量的加法运算法则的应用，是基础题．
练习册系列答案
相关题目
8．函数f（x）=x2+ax+5，对x∈R恒有f（x）=f（-4-x），若x∈[m，0]（m＜0）时，f（x）的值域为[1，5]，则实数m的取值范围是（ ）
| A． | [-4，-2] | B． | （-4，0） | C． | [-4，0] | D． | [-2，0] |
9．函数 y=3-$\frac{3}{1-x}$（ ）
| A． | 在（-1，+∞）内单调递增 | B． | 在（-1，+∞）内单调递减 | ||
| C． | 在（1，+∞）内单调递增 | D． | 在（1，+∞）内单调递减 |
6．若n∈N且n为奇数，则6n+C${\;}_{n}^{1}$6n-1+C${\;}_{n}^{2}$6n-2+…+C${\;}_{n}^{n-1}$6-1被8除所得的余数是（ ）
| A． | 0 | B． | 2 | C． | 5 | D． | 7 |
13．命题“?x∈R，f（x）＞0”的否定为（ ）
| A． | ?x0∈R，f（x0）＞0 | B． | ?x0∈R，f（x0）≤0 | C． | ?x0∈R，f（x0）≤0 | D． | ?x0∈R，f（x0）＞0 |
3．不等式$\sqrt{a^2-x^2}$＜x+a（a＞0）的解集是（ ）
| A． | {x|-$\frac{a}{2}$＜x＜a} | B． | {x|x＞0或x$＜-\frac{3}{5}$a} | ||
| C． | {x|-a≤x≤-$\frac{3}{5}$a或0≤x＜a} | D． | {x|0＜x≤a} |
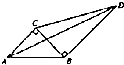如图，在平面内将四块直角三角板接在一起，已知∠ABC=45°，∠BCD=60°，记$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$．
7．已知集合A={x|（x-1）（x-3）＜0}，B={x|2＜x＜4}，则A∩B=（ ）
| A． | {x|2＜x＜3} | B． | {x|1＜x＜3} | C． | {x|3＜x＜4} | D． | {x|1＜x＜4} |