题目内容
【题目】已知函数![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)已知![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)对于在![]() 中的任意一个常数
中的任意一个常数![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() ,请说明理由。
,请说明理由。
【答案】(1) ![]() (2)
(2) ![]() (3)见解析
(3)见解析
【解析】
(Ⅰ)根据导数几何意义列式可得方程组,解得![]() 的值;(Ⅱ)先化简不等式,再研究函数
的值;(Ⅱ)先化简不等式,再研究函数![]() 最小值,利用导数易得函数
最小值,利用导数易得函数![]() 单调性,由单调性得最小值,解不等式得结果;(Ⅲ)先化简不等式,再研究函数
单调性,由单调性得最小值,解不等式得结果;(Ⅲ)先化简不等式,再研究函数![]() 最小值,利用导数易得函数
最小值,利用导数易得函数![]() 单调性即得最小值
单调性即得最小值![]() ,最后再利用导数证明
,最后再利用导数证明![]() .
.
(Ⅰ)解:函数![]() 的导数为
的导数为![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]() ,可得
,可得![]() ,
,
所以函数的切线方程为![]() ,即
,即![]() ,
,
所以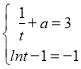 ,解得
,解得![]() .
.
(Ⅱ)证明:由(Ⅰ)可得![]() ,
,
因为![]() ,所以
,所以![]() ,即为
,即为![]()
可令![]() ,
,
由![]() ,
,![]() ,可得
,可得![]() ,即有
,即有![]() ,
,![]() 在
在![]() 递增,
递增,
可得![]() ,所以
,所以![]() ,故
,故![]() 的取值范围为
的取值范围为![]() ;
;
(Ⅲ)解:对于在![]() 中的任意一个常数
中的任意一个常数![]() ,
,
假设存在正数![]() ,使得:
,使得:![]() .
.
由![]() 成立,
成立,
从而存在正数![]() ,使得上式成立,只需上式的最小值小于
,使得上式成立,只需上式的最小值小于![]() 即可.
即可.
令![]() ,
,
![]()
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
则![]() 为函数
为函数![]() 的极小值,即为最小值点.
的极小值,即为最小值点.
故![]() 的最小值为
的最小值为
![]() ,
,
再令![]()
![]()
则![]() 在
在![]() 递增,可得
递增,可得![]() ,则
,则![]() .
.
故存在正数![]() ,使得
,使得![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目