题目内容
8.已知cos(x-$\frac{1}{3}$π)=$\frac{1}{4}$,求sin($\frac{2π}{3}$+x)的值$±\frac{\sqrt{15}}{4}$.分析 直接利用诱导公式化简已知条件求出所求表达式的值即可.
解答 解:cos(x-$\frac{1}{3}$π)=$\frac{1}{4}$,
可得cos($\frac{2π}{3}$+x)=-$\frac{1}{4}$,
sin($\frac{2π}{3}$+x)=±$\sqrt{1-{cos}^{2}(\frac{2π}{3}+x)}$=±$\frac{\sqrt{15}}{4}$.
故答案为:±$\frac{\sqrt{15}}{4}$.
点评 本题考查诱导公式的应用,考查计算能力.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
19.下列命题中不正确的是( )
| A. | logab•logbc•logca=1(a,b,c均为不等于1的正数) | |
| B. | 若xlog34=1,则${4^x}+{4^{-x}}=\frac{10}{3}$ | |
| C. | 函数f(x)=lnx满足f(a+b)=f(a)•f(b)(a,b>0) | |
| D. | 函数f(x)=lnx满足f(a•b)=f(a)+f(b)(a,b>0) |
13.函数y=xsinx的部分图象是( )
| A. | 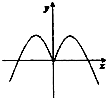 | B. | 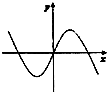 | C. | 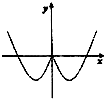 | D. | 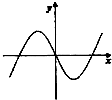 |
17.解不等式组:$\left\{\begin{array}{l}{2(x-6)>3-x}\\{\frac{2x-1}{3}-\frac{5x+1}{2}≤1}\end{array}\right.$.
11.建造一个容积为2m3,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为( )
| A. | 660 | B. | 760 | C. | 670 | D. | 680 |