题目内容
3.在△ABC中,A=120°,则sinB+sinC的最大值为1.分析 根据两角和差的正弦公式得到sinB+sinC=sin(60°+C),根据0<C<60°的范围即可求出.
解答 解:∵△ABC中,A=120°,
∴sinB+sinc=sin(180°-120°-C)+sinC,
=sin(60°-C)+sinC,
=sin60°cosC-cos60°sinC+sinC,
=$\frac{\sqrt{3}}{2}$cosC+$\frac{1}{2}$sinC,
=sin60°cosC+cos60°sinC,
=sin(60°+C),
∵0<C<60°,
∴60°<60°+C<120°,
当60°+C=90°时,sin(60°+C)最大,最大值为1,
故答案为;1.
点评 本题考查了两角和差的正弦公式,和解三角形的有关问题,关键是化简,属于基础题.

练习册系列答案
相关题目
13.下列四组函数中,表示相等函数的是( )
| A. | f(x)=$\sqrt{x}$,g(x)=($\sqrt{x}$)2 | |||||||||
| B. | f(x)=2lgx,g(x)=lgx2 | |||||||||
| C. | f(x)=$\sqrt{x-1}$$\sqrt{x+1}$,g(x)=$\sqrt{{x}^{2}-1}$ | |||||||||
| D. | f(x)=$\left\{\begin{array}{l}{1,x≤1}\\{2,1<x<2}\\{3,x≥2}\end{array}\right.$,
|



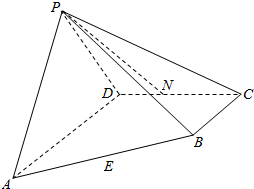 如图,四棱锥P-ABCD的侧面PAD垂直于底面ABCD,∠ADC=∠BCD=90°,PA=PD=AD=2BC=2,CD=$\sqrt{2}$,N为线段CD的中点.
如图,四棱锥P-ABCD的侧面PAD垂直于底面ABCD,∠ADC=∠BCD=90°,PA=PD=AD=2BC=2,CD=$\sqrt{2}$,N为线段CD的中点.