题目内容
11.建造一个容积为2m3,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为( )| A. | 660 | B. | 760 | C. | 670 | D. | 680 |
分析 设出池底的两边长分别为x、y米,依据体积公式得到2xy=2,及水池的总造价关系式z=120xy+2×(2x+2y)×80,化为z=320(x+y)+120,依据基本不等式即可求出.
解答 解:设池底的一边长为x米,另一边长为y米,总造价为z元,依题意有
2xy=2,①
z=120xy+2×(2x+2y)×80,②
由①得xy=1,代入②得z=320(x+y)+120≥320×2$\sqrt{xy}$+120=760,当且仅当x=y=1时取“=”号.
所以当池底的长、宽都为1m时才能使水池的总造价最低,最低的总造价为760元.
点评 本题考查利用数学知识解决实际问题,考查基本不等式的应用,使用时要注意“一正,二定,三相等”.

练习册系列答案
相关题目
20.已知焦点在y轴上的双曲线C的一条渐近线与直线$l:x+\sqrt{3}y=0$垂直,且C的一个焦点到l的距离为3,则C的标准方程为( )
| A. | $\frac{y^2}{9}-\frac{x^2}{3}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{3}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{6}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{6}=1$ |
1.已知命题p:?x>0,总有(x+1)ex>1,则¬p为( )
| A. | ?x0≤0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | B. | ?x0>0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | ||
| C. | ?x0>0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | D. | ?x0≤0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 |
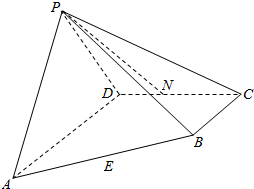 如图,四棱锥P-ABCD的侧面PAD垂直于底面ABCD,∠ADC=∠BCD=90°,PA=PD=AD=2BC=2,CD=$\sqrt{2}$,N为线段CD的中点.
如图,四棱锥P-ABCD的侧面PAD垂直于底面ABCD,∠ADC=∠BCD=90°,PA=PD=AD=2BC=2,CD=$\sqrt{2}$,N为线段CD的中点.