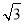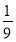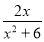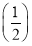题目内容
已知函数f(x)=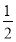 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R.
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)求f(x)的单调区间.
(1)a=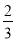 (2)f(x)的单调递增区间是
(2)f(x)的单调递增区间是 和(2,+∞),单调递减区间是
和(2,+∞),单调递减区间是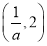
【解析】f′(x)=ax-(2a+1)+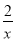 (x>0).
(x>0).
(1)由题意得f′(1)=f′(3),解得a=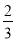 .
.
(2)f′(x)= (x>0).
(x>0).
①当a≤0时,x>0,ax-1<0.在区间(0,2)上,f′(x)>0;在区间(2,+∞)上,f′(x)<0,故f(x)的单调递增区间是(0,2),单调递减区间是(2,+∞).
②当0<a< 时,
时,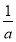 >2.在区间(0,2)和
>2.在区间(0,2)和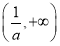 上,f′(x)>0;在区间
上,f′(x)>0;在区间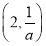 上,f′(x)<0.
上,f′(x)<0.
故f(x)的单调递增区间是(0,2)和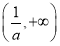 ,单调递减区间是
,单调递减区间是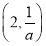 .
.
③当a=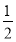 时,f′(x)=
时,f′(x)= ≥0,
≥0,
故f(x)的单调递增区间是(0,+∞).
④当a>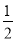 时,0<
时,0<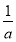 <2,在区间
<2,在区间 和(2,+∞)上,f′(x)>0;在区间
和(2,+∞)上,f′(x)>0;在区间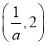 上,f′(x)<0.
上,f′(x)<0.
故f(x)的单调递增区间是 和(2,+∞),单调递减区间是
和(2,+∞),单调递减区间是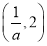 .
.

练习册系列答案
相关题目