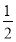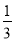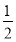Question

已知函数f(x)＝ex－ln(x＋m)．

(1)设x＝0是f(x)的极值点，求m，并讨论f(x)的单调性；

(2)当m≤2时，证明f(x)>0.

 

Answer 1

（1）1（2）见解析

【解析】f′(x)＝ex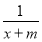－，由x＝0是f(x)的极值点，得f′(0)＝0，所以m＝1，

于是f(x)＝ex－ln(x＋1)，定义域为{x|x>－1}，

f′(x)＝ex－，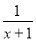

函数f′(x)＝ex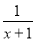－在(－1，＋∞)上单递增，

且f′(0)＝0，

因此当x∈(－1,0)时，f′(x)<0；

当x∈(0，＋∞)时，f′(x)>0.

所以f(x)在(－1,0)上单调递减，在(0，＋∞)上单调递增．

(2)证明　当m≤2，x∈(－m，＋∞)时，ln(x＋m)≤ln(x＋2)，故只需证明当m＝2时，f(x)>0，

当m＝2时，函数f′(x)＝ex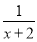－在(－2，＋∞)上单调递增．

又f′(－1)<0，f′(0)>0，故f′(x)＝0在(－2，＋∞)上有唯一实根x0，且x0∈(－1,0)．

当x∈(－2，x0)时，f′(x)<0；当x∈(x0，＋∞)时，f′(x)>0，从而当x＝x0时，f(x)取得最小值．

由f′(x0)＝0，得ex0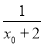＝，即ln(x0＋2)＝－x0，故f(x)≥f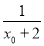(x0)＝＋x0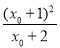＝ >0.综上，当m≤2时，f(x)>0.